Объяснение:
Найдем угол А: 90 - 27 = 63 градуса(сумма острых углов в прямоугольном треугольнике равна 90 градусов).
Найдем гипотенузу AB.
Синус угла A равен отношению противолежащего данному углу катета BC к гипотенузе AB.
Иначе говоря:
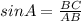
Синус 63 градусов равен 0,891007.
Выразим из этой формулы AB:
AB = BC/sinA = 13/0,891007 = 14,6
Для того, чтобы найти катет AC, мы должны использовать тангенс, т.к. именно эта тригонометрическая функция связывает оба катета.

Тангенс - это отношение противолежащего катета к прилежащему.
Тангенс 27 градусов равен 0,21.
Чтобы найти AC, мы тангенс угла B умножим на BC.
AC = tgB * BC = 0,51 * 13 = 6,63
Пусть DB - x (сторона AB разделенная высотой), тогда AD=BC=3-x, т.к. CD - высота,то для прямоугольного ΔDBC мы можем найти гипотунузу BC:
(√3)²+х²=(3-х)²
3+х²=9-6х+х²
6х=6
х=1 - сторона DB => AD= 3-1=2
Теперь когда известна сторона AD можем найти гипотенузу AC для треугольника ADC:
AC²=2²+(√3)²=4+3=7 => AC=√7
все просто