Відповідь:
182.79644736
Пояснення:
Знайдемо сторону квадрата а, вписаного в круг
а=R√2
Тоді, площа меншого сегмента обрахофується за формулою
S=R^2×arcsin(a/(2R))-a/4×√(4R^2-a^2)
S=64arcsin(8√2/16)-8√2/4×√(4×64-2×64)=64arcsin(√2/2)-2√2×8√2=64×pi/4-32=16pi-32 =18.265482457
Площе сегмента можна вирахувати як площу сектора- площу трикутника, яка дорівнює четвертій частині площі квадрата
Площа сектора, так як кут між діагоналями квадрата дорівнює 90°=рі/2, дорівнює
S=pi/2×R^2/2-a^2/4=16pi-32
Знайдемо площу кола
S○=pi×R^2=pi×64=201.06192982
Тоді більший сектор буде різницею площі кола й меншого сектора
S◐=S○-S=201.06192982-18.265482457 =182.79644736=58pi
Объяснение:
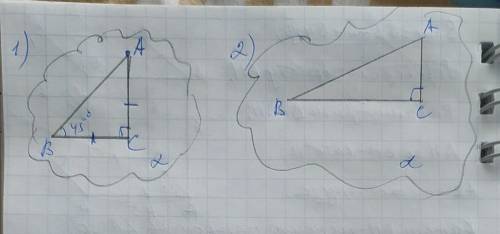
1) позначемо похилу АВ, проекцію ВС, відстань від точки А до площини - АС - отримаємо прямокутний трикутник АВС, в якому ВС і АС - катети, а АВ - гіпотенуза. Якщо ВС=АС, тоді отриманий трикутник АВС - рівнобедренний, тому його кути при основі АВ - рівні. Так як сума гострих кутів прямокутного трикутника дорівнює 90°, тоді кутА=кутВ=90÷2=45°
ВІДПОВІДЬ: кутВ між площиною та похилою дорівнює 45°
2) Так само позначемо кути, як у першому завданні АВС, і якщо катет АС дорівнює половині гіпотенузи АВ, тоді АС лежить навпроти кута В=30°(властивість кута 30°),
ВІДПОВІДЬ: кутВ=30°