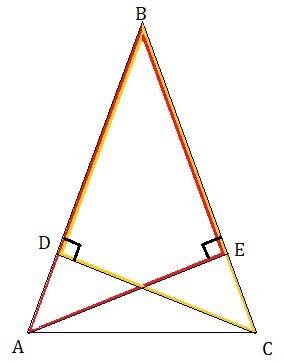
∠BEA = ∠BDC = 90° (так как AE и CD — высоты △ABC).
⟹ треугольники ABE и CBD прямоугольные.
Сумма острых углов прямоугольного треугольника равна 90°.
В треугольнике ABE ∠BAE = 90° — ∠B.
В треугольнике CBD ∠BCD = 90° — ∠B.
⟹ ∠BAE = ∠BCD, ∠B — общий,
BA = BC (как боковые стороны равнобедренного △ABC)
Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
⟹ треугольники ABE и CBD равны.
Из равенства треугольников следует равенство соответствующих сторон: AE = CD.
Что и требовалось доказать.
Решение: Рассмотрим треугольник ACH: Так как CH - высота,то этот треугольник прямоугольный. Следовательно CH - катет и мы находим его по теореме Пифагора: CH = √6^²-4^² = √36-16 = √20 = 2√5
Я предлагаю рассмотреть треугольник ABC и найти x через CB(не знаю можно ли так,как я решил,но я запишу)
AB=4+x
CB=√AB²-AC² = √(4-x)²-6² = √x²-10x-20
Разбираем квадратичное уравнение:
x²-10x-20=0
D= 100+4*20=180 √D= 6√5
x_{12} = 5+-3√5
x2 - не подходит,так как получается отрицательным,поэтому BH = 5+3√5.
ответ: 5+3√5