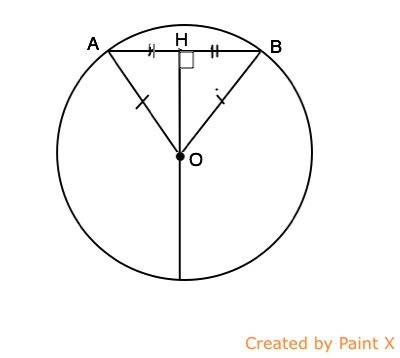
Соединим центр О окружности с концами хорды АВ. ОА=ОВ=R.
Треугольник АОВ - равнобедренный. Проведем высоту ОН этого треугольника.
Угол ОНВ=углу ОНА=90º
«Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один»
Следовательно, и к середине хорды можно провести только один перпендикуляр.
Высота ОН - медиана равнобедренного треугольника.
АН=ВН. Точка Н - середина АВ.
Следовательно, ОН, проходящий через середину АВ, есть срединный перпендикуляр хорды АВ, ч.т.д.
R= 3 см
Правильный четырехугольник- это квадрат.
Найти: S-?
Решение:
Точка пересечения диагоналей квадрата и центр окружности, описанной вокруг него, совпадают. Отсюда можно сделать вывод, что диагональ квадрата- это диаметр окружности, а полудиагональ- радиус окружности.
Sкв= a^2, где а- это сторона квадрата.
Сторона квадрата, вписанного в окружность находится по формуле: а= R*sqrt(2).
*sqrt- корень квадратный
Подставляем в формулу.
Sкв= (R*sqrt(2))^2=(3*sqrt(2))^2= 9*2=18 см^2
ответ: 18 см^2