Объяснение:
Обозначим вершины треугольника АВС с прямым углом С и высотой СН.
Найдём по теореме Пифагора катет АС:
4) АС²=АВ²–ВС²=50²–30²=2500–900=1600
АС=√1600=40см
Высота, проведённая из вершины прямого угла делит ∆АВС на 2 треугольника, подобных данному и подобными между собой.
Рассмотрим ∆АВС и ∆АСН.
Пусть СН=х.
В нём соответсаующие стороны будут пропорциональны, составим пропорцию:

Перемножим крест накрест:
50х=30×40
50х=1200
х=1200÷50
х=24см
ОТВЕТ: СН=24см
5) Вычислим по формуле суммы углов многоугольника, где n – количество сторон
180(n–2)=135n
180n–360=135n
180n–135n=360
45n=360
n=360÷45
n=8
ОТВЕТ: 8 сторон

Объяснение:
Обозначим пересечение диагоналей точкой О. Диагонали параллелограмма точкой пересечения делятся пополам, поэтому АО=СО=12÷2=6(ед), а ВО=ДО=10÷2=5(ед).
Для нахождения ∠АОВ воспользуемся теоремой косинусов:
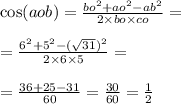
cos(1/2)=60°
ОТВЕТ: ∠АОВ=60°
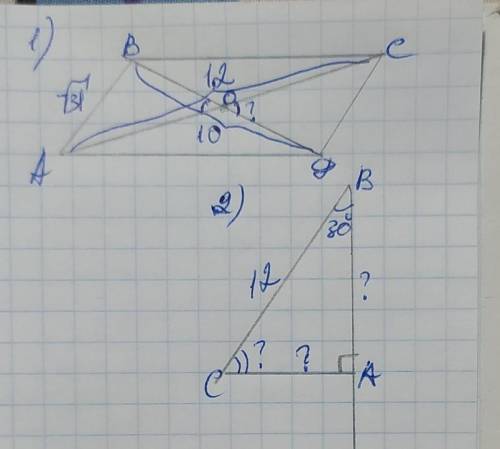
2) Сумма острых углов прямоугольного треугольника равна 90°, поэтому
∠С=90–∠В=90–30=60°
∠С=60°
Катет АС лежит напротив угла 30°, поэтому он равен половине гипотенузы ВС:
АС=ВС÷2=12÷2=6(ед)
По теореме Пифагора:
АВ²=ВС²–АС²=12²–6²=144–36=108
АВ=√108=6√3(ед)
ОТВЕТ: АС=6(ед); АВ=6√3(ед); ∠С=60°
х(5х-3)=26
х(5х-3)=2•13