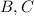 отрезки
отрезки 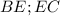 , где точка
, где точка 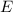 пересечение с окружностью. Обозначим точку перпендикуляра
пересечение с окружностью. Обозначим точку перпендикуляра 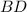 с
с 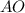
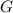 .
. 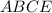 , который вписан в окружность.
, который вписан в окружность. 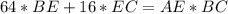 , так как
, так как 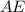 лежит на центре , то треугольники
лежит на центре , то треугольники 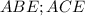 прямоугольные.
прямоугольные. 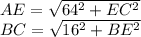 .
. 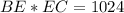 .
. 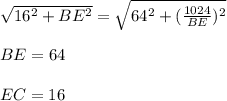
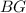 - высота прямоугольного треугольника
- высота прямоугольного треугольника 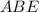 , тогда
, тогда 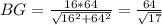 .
.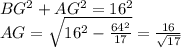 , так как
, так как 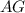 является высотой прямоугольного треугольника
является высотой прямоугольного треугольника 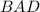 , то
, то 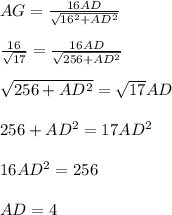
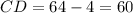
Находим площадь треугольника:
S = √(p(p-a)(p-b)(p-c)) = √(21* 8* 7* 6) = √ 7056 = 84 см².
Тогда радиус вписанной окружности равен:
r = S/p = 84/21 = 4 см.
Отсюда находим искомое расстояние точки М от плоскости треугольника АВС:
Н = √(5² - r²) = √(25 - 16) = √9 = 3 см.