Для даної задачі треба скористатися властивостями катетів та їх проекцій на гіпотенузу в прямокутному трикутнику.
Перший б
Катет прямокутного трикутника — середнє пропорційне між гіпотенузою  і проекцією цього катета на гіпотенузу:
і проекцією цього катета на гіпотенузу:
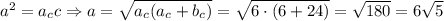 см
см
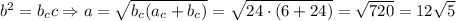 см
см
Площа 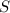 прямокутного трикутника знаходится як півдобуток його катетів:
прямокутного трикутника знаходится як півдобуток його катетів:
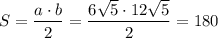 см²
см²
Другий б
Висота 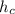 прямокутного трикутника, що проведена до гіпотенузи
прямокутного трикутника, що проведена до гіпотенузи  з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
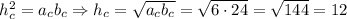 см
см
Площа 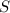 будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи
будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи  і висоти
і висоти 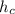 , що до неї проведена:
, що до неї проведена:
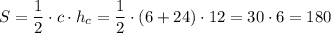 см²
см²
Відповідь: 180 см².
Украинский:
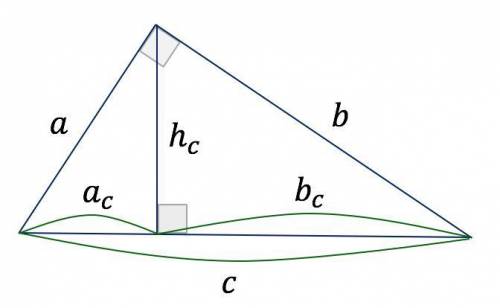
трикутник АВС, кут = 90, ВС - гіпотенуза, АН-висота на ВС, ВН = 28, СН = 7
ВН / АН = АН / НС. 28 / АН = АН / 7, АН в квадраті = 196, АН = 14
АС = корінь (АН в квадраті + НС в квадраті) = корінь (196 + 49) = корень245 = 7 х корень5
АВ = корінь (АН в квадраті + ВН в квадраті) = корінь (196 + 784) = корень980 =
= 14 х корень5
Площа = 1/2 х АС х АВ = 1/2 х 7 х корень5 х 14 х корень5 = 245
Русский:
треугольник АВс, уголА=90, ВС - гипотенуза, АН-высота на ВС, ВН=28, СН=7
ВН/АН=АН/НС. 28/АН=АН/7, АН в квадрате = 196, АН=14
АС = корень(АН в квадрате + НС в квадрате) = корень(196 + 49) =корень245 =7 х корень5
АВ = корень (АН в квадрате + ВН в квадрате) = корень(196 + 784) = корень980 =
=14 х корень5
Площадь = 1/2 х АС х АВ = 1/2 х 7 х корень5 х 14 х корень5 = 245
1. Пусть АМ = х, тогда СМ = 3 - х.
(3 - x) : x = 3 : 2
6 - 2x = 3x
5x = 6
x = 1,2
AM = 1,2 см, СМ = 1,8 см
2. Так как MN < NK, то MP < PK.
Пусть МР = х, тогда РК = х + 0,5
4 : x = 5 : (x + 0,5)
5x = 4x + 2
x = 2
МР =2 см, РК = 2,5 см
3. DE + EP = Pdep - DP = 21 - 7 = 14 см
Пусть DE = x, тогда ЕР = 14 - х
x : 3 = (14 - x) : 4
4x = 42 - 3x
7x = 42
x = 6
DE = 6 см, ЕР = 8 см
4. Пусть АВ = х, тогда ВС = х + 3.
x : 2 = (x + 3) : 3
3x = 2x + 6
x = 6
АВ = 6 см, ВС = 9 см
6. В условии опечатка: надо найти длины сторон CD и DE.
DF - диагональ ромба, а диагонали ромба лежат на биссектрисах его углов, значит DF - биссектриса треугольника.
CD + DE = Pcde - CE = 55 - 20 = 35 см
Пусть CD = х, тогда DE = 35 - х
x : 8 = (35 - x) : 12
12x = 280 - 8x
20x = 280
x = 14
CD = 14 см, DE = 21 см
7. ΔАВС, ∠С = 90°, АМ - биссектриса.
Пусть АС = х, тогда по теореме Пифагора АВ = √(х² + 81).
x : 4 = √(х² + 81) : 5
5x = 4√(х² + 81)
25x² = 16x² + 81 · 16
9x² = 81 · 16
x² = 9 · 16
x = 3 · 4 = 12
АС = 12 см
Sabc = AC · CB / 2 = 12 · 9 = 54 см²
8. Так как точка О равноудалена от катетов, СО - диагональ квадрата, а диагонали квадрата лежат на биссектрисах его углов. Значит СО - биссектриса треугольника.
а : 40 = b : 30
b = 30a / 40 = 3a/4
По теореме Пифагора:
70² = a² + 9a²/16
25a²/16 = 4900
a² = 4900 · 16 / 25 = 196 · 16
a = 14 · 4 = 56
CB = 56 см
АС = 3 · 56 / 4 = 3 · 14 = 42 см
Sabc = CB · AC / 2 = 56 · 42 / 2 = 1176 см²
9. ΔАВС: ∠В = 60°, ∠С = 40°, ⇒ ∠А = 80°.
О - точка пересечения биссектрис.
∠ОАС + ∠ОСА = (∠А + ∠С)/2 = (80° + 40°)/2 = 60°
Из ΔОАС ∠АОС = 180° - (∠ОАС + ∠ОСА) = 180° - 60° = 120°
10. ΔАВС с прямым углом С, СМ - биссектриса.
АС = АВ/2 = 2 см как катет, лежащий напротив угла в 30°.
По теореме Пифагора
ВС = √(АВ² - АС²) = √(16 - 4) = √12 = 2√3 см
Пусть АМ = х, тогда МВ = 4 - х.
x : 2 = (4 - x) : (2√3)
2√3x = 8 - 2x
2x(√3 + 1) = 8
x = 4 / (√3 + 1) = 4(√3 - 1) / (3 - 1) = 2(√3 - 1)
AM = 2(√3 - 1) см
МВ = 4 - (2√3 - 2) = 6 - 2√3 = 2√3(√3 - 1) см
11. ΔАВС: ∠С = 90°, ∠А = 60°, ⇒ ∠В = 30°, тогда
АВ = 2АС = 2√3 см по свойству катета, лежащего напротив угла в 30°.
По теореме Пифагора:
ВС = √(АВ² - АС²) = √(12 - 3) = √9 = 3 см
СМ - биссектриса.
Пусть АМ = х, МВ = 2√3 - х.
x : √3 = (2√3 - x) : 3
3x = 6 - √3x
x(3 + √3) = 6
x = 6 / (3 + √3) = 6(3 - √3) /(9 - 3) = 3 - √3 = √3(√3 - 1)
AM = √3(√3 - 1) см
МВ = 2√3 - 3 + √3 = 3√3 - 3 = 3(√3 - 1) см