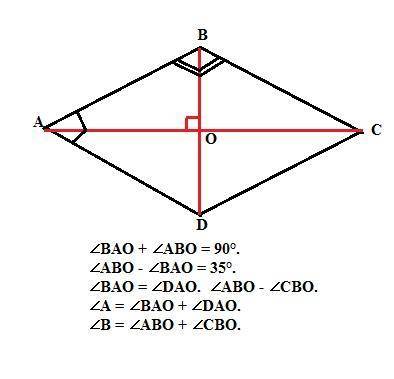
∠A = ∠C = 55° и ∠B = ∠D = 125°.
Объяснение:
Диагонали ромба взаимно перпендикулярны. Следовательно, они со стороной ромба образуют прямоугольный треугольник. Сумма острых углов прямоугольного треугольника равна 90°, а их разность равна 35° (дано).
Пусть один из углов равен х градусов. Тогда второй равен х+35 градусов.
Значит 2х = 90-35 = 55°. И один из углов треугольника равен 55:2 = 27,5°.
Тогда второй угол равен 27,5+35 = 62,5°.
В ромба диагонали являются биссектрисами его углов. Следовательно, углы ромба равны удвоенным градусным мерам найденных углов прямоугольного треугольника.
Противоположные углы ромба равны.
Углы ромба равны 125° и 55°.
Проверка: углы ромба, прилежащие к одной стороне, в сумме равны 180°.
125+55 = 180°.


AH=1/2AB⇒<ABH=30⇒<A=90-30=60
<B=180-<A=180-60=120
AB=BH/sin60=8:√3/2=16/√3см
<ABD=<CBD=1/2<B=60⇒ΔABD-равносторонний⇒BD=16/√3см
S=AD*BH=BD*AC
AC=AD*BH/BD=BH=8