Только из за Пифагоровых треугольников :) и никаких чертежей :)
Треугольник со стронами 25, 29, 36 составлен из двух прямоугольных целочисленных треугольников со сторонами 15, 20, 25 и 20, 21, 29. Эти треугольники приставлены друг к другу равными катетами 20 таким образом, что катеты 15 и 21 вместе образуют сторону 36 исходного треугольника. (этот "хитрый" прием на самом деле не обязателен, но очень полезен - с ним трудно ошибиться :)
Поэтому высота треугольника к стороне 36 равна 20, площадь 360, а высота к стороне 25 равна 2*360/25 = 28,8; Обозначим это высоту L.
Вращение треугольника производится таким образом, что сторона 25 является осью вращения. При этом стороны 29 и 36 являются образующими двух конусов с радиусами оснований L. Поэтому их суммарная площадь (площадь боковых поверхностей двух конусов) будет равна
S = пи*L*29 + пи*L*36 = пи*28,8*65 = пи*144*13 = 1872*пи
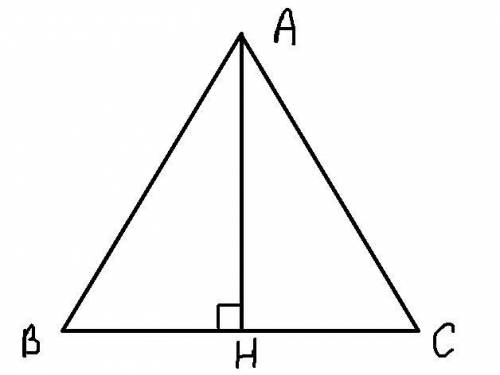
(Смотри вложение)
S = 0,5 * BC * AH
Т.к. ΔABС - равносторонний ⇒ AH является не только высотой, но и биссектрисой и медианой. Из этого можно сделать вывод, что ∠BAH = ∠CAH = 30° и BH=СН
Рассмотрим ΔABH
ΔABH - прямоугольный, т.к. AH -высота
Пусть х - BH, тогда 2х - ВА (т.к. треугольник ΔABС равносторонний и сторона, лежащая напротив ∠ 30° равна половине гипотенузы), тогда по т. Пифагора:
х² + (12√3)² = (2х)²
х² - 4х² + 432 = 0
-3х² = - 432 | : (-3)
х² = 144
x = 12 ( корень -12 мы не берём, т.к. сторона треугольника не может быть отрицательной)
Получается ВС = 2 * ВН = 2*12 = 24
S = 0,5 * 24 * 12√3 = 12 * 12√3 = 144√3 см²
ответ: S = 144√3 см²
прости за некачественный рисунок. в расчетах мог и ошибиться. но ход решения верный.