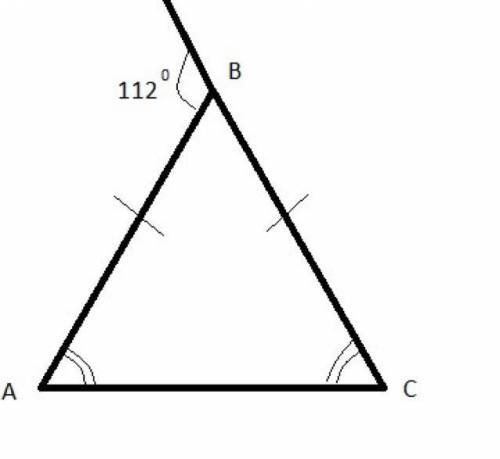
а) Треугольник АВС равнобедренный с боковыми сторонами АВ=ВС. б) В треугольнике АВС: ∠А = ∠С = 70°, ∠В = 40°.
Объяснение:
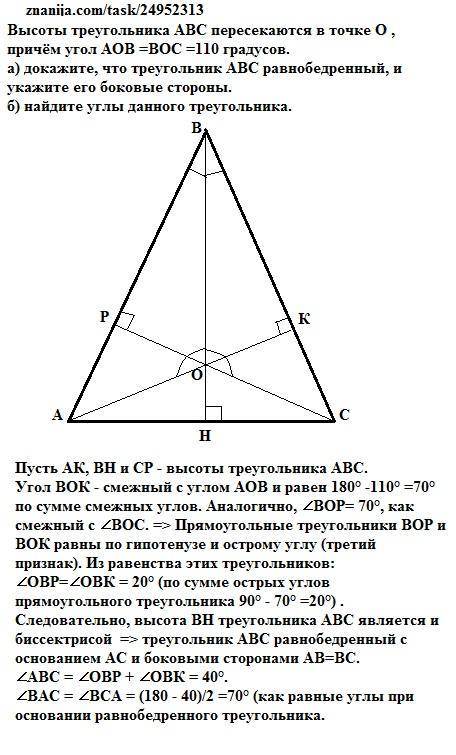
Пусть АК, ВН и СР - высоты треугольника АВС.
Угол ВОК - смежный с углом АОВ и равен 180° -110° =70°по сумме смежных углов. Аналогично, ∠ВОР= 70°, как смежный с ∠ВОС. => Прямоугольные треугольники ВОP и ВОК равны по гипотенузе и острому углу (третий признак). Из равенства этих треугольников:
∠ОВР=∠ОВК = 20° (по сумме острых углов прямоугольного треугольника 90° - 70° =20°) .
Следовательно, высота ВН треугольника АВС является и биссектрисой => треугольник АВС равнобедренный с основанием АС и боковыми сторонами АВ=ВС. Что и требовалось доказать.
∠АВС = ∠ОВР + ∠ОВК = 40°.
∠ВАС = ∠ВСА = (180 - 40)/2 =70° (как равные углы при основании равнобедренного треугольника.
итак... если провести биссектрису и посчитать углы у двух новых треугольников АСД и ДСВ,получается, что угол СДВ=60градусов -->угол АДС=180-60=120 градусов. угол А= 180-120-45=15... так. sin15~=0,258 ищем АВ.sin15=CB/AB -->AB=4корня из 6/0,258~=15корней из 6 есть такая формула: CB*CB=AB*BD ---> BD= корень из СВ*СВ/АВ=96/15корн из 6=32/5корней из 6
не знаю ответ,но пожет быть и такой странный,или преобразуй его как -нибудь