№49: DK = 2
№50: MD = 16
Объяснение:
№49:
Т.к. ABCD - параллелограмм, AB || CD, то есть AB || CK. Тогда BK - секущая при параллельных прямых. Следовательно, ∠ABK=∠BKC, как накрест лежащие углы при параллельных прямых. Рассмотрим треугольник BCK: ∠CBK=∠BKC (∠ABK=∠CBK, по условию, а ∠ABK=∠BKC), следовательно, треугольник BCK равнобедренный. По свойству равнобедренного треугольника боковые стороны равны, то есть BC = CK = 8 (по условию). BC = CD + DK, CD = AB = 6 (по свойству параллелограмма), тогда DK = BC - CD = 8 - 6 = 2.
№50:
Т.к. ABCD - параллелограмм, BC || AD, то есть BC || MD. Тогда CM - секущая при параллельных прямых. Следовательно ∠BCM=∠CMA, как накрест лежащие углы при параллельных прямых.. Рассмотрим треугольник CAM: ∠CMA=∠MCA (∠MCA = ∠BCM по условию, а ∠BCM=∠CMD), следовательно, треугольник CAM равнобедренный. По свойству равнобедренного треугольника боковые стороны равны, то есть AM = AC = 10 (по условию). MD = AM + AD, BC = AD = 6 (по свойству параллелограмма), тогда MD = AM + AD = 10 + 6 = 16.
Дано:
параллелепипед ABCDA1B1C1D1
AC = A1C1 = 6 см
BD = B1D1 = 8 см
AA1 = DD1 = CC1 = DD1 = 7 см
1. Рассмотрим ромб ABCD, лежащий в основании. По свойствам ромба, его диагонали пересекаются под прямым углом и точкой пересечения делятся попопам. Обозначим точку пересечения как O.
2. Рассмотрим треугольник AOD. Он прямоугольный, его катеты AO и OD.
AO = AC/2 = 6/2 = 3 см
OD = BD/2 = 8/2 = 4 см
Найдем гипотенузу AD:
AD =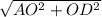
AD = 5 см
3. Стороны ромба равны, значит, треугольник AOD = AOB = BOC = COD, AB = BC = CD = AD = 5 см.
4. Теперь мы знаем все грани и можем найти площади.
Площадь оснований (площади ромбов) ABCD и A1B1C1D1 рассчитываются по формуле:
S = (AD * BC)/2 = 24 кв.см
Площади граней (всех в силу равенства сторон) - как площади прягоугольников.
S = AA1 * AB = 7 * 5 = 35 кв.см
5. Площадь полной поверхности:
S = 2 * 24 + 4 * 35 = 48 + 140 = 188 кв.см
ответ: S = 188 кв.см
Вот и все :) Удачи!