Объяснение:
Обратим внимание на то, что ON и OM являются перпендикулярами к катетам прямоугольного треугольника, поскольку нам необходимо найти расстояние KN и KM.
Рассмотрим отрезок NO. Он является перпендикуляром к CB. Угол ACB также вляется прямым по условию задачи. Таким образом, треугольники ABC и OBN - подобны по признаку равенства углов (см. подобие треугольников). Угол В - общий, а, поскольку CA и NO являются перпендикулярами к CB - то остальные углы также равны (один прямой, второй равен 180 градусов минус сумма остальных углов, равенство которых мы уже доказали).
Коэффициент подобия треугольников равен соотношению BO к BA. Поскольку точка О - точка касания медианы прямоугольного треугольника к гипотенузе, то есть AO = OB, то коэффициент подобия будет равен 1:2.
Откуда ON = CA / 2 = 9 / 2 = 4,5
Расстояние же KN найдем по теореме Пифагора.
KN = √(4,52 + 62 ) = 7,5 см
Аналогично, найдем расстояние до второго катета:
OM = CB / 2 = 12 / 2 = 6
KN = √( 62 + 62 ) = √72 = 6√2 см
ответ: 7,5 см, 6√2 см
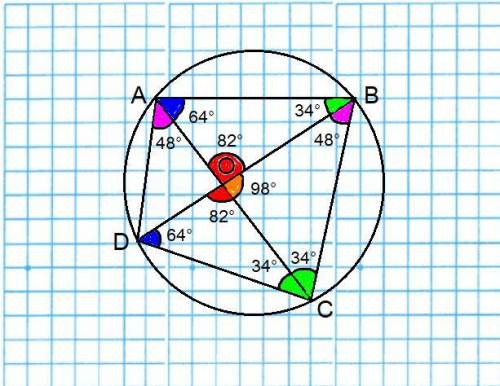
ответ: ∠A = 112° ; ∠B = 82° ; ∠C = 68° ; ∠D = 98°.
Объяснение: Обозначим середину окружности буквой O.
∠CBD и ∠CAD - вписанные (углы, у которых вершина на окружности, а стороны пересекают окружность).
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
⇒ ∠CBD = ∠CAD = 48°.
COD - треугольник.
Сумма внутренних углов треугольника равна 180°.
⇒ ∠DOC = 180° - (64° + 34°) = 180° - 98° = 82°.
Сумма смежных углов равна 180°.
⇒ ∠BOC = 180° - 82° = 98°.
COB - треугольник.
Сумма внутренних углов треугольника равна 180°.
⇒ ∠OCB = 180° - (98° + 48°) = 180° - 146° = 34°.
⇒ ∠C = 34° * 2 = 68°.
Если четырёхугольник можно вписать в окружность, то сумма противоположных углов этого четырёхугольника равна 180°.
⇒ ∠A = 180° - 68° = 112°.
Если ∠CAD = 48° и ∠A = 112° ⇒ ∠CAB = 112° - 48° = 64°.
Вертикальные углы равны.
⇒ ∠DOC = ∠AOB = 82°.
AOB - треугольник.
Сумма внутренних углов треугольника равна 180°.
⇒ ∠ABO = 180° - (64° + 82°) = 180° - 146° = 34°.
⇒ ∠B = 34° + 48° = 82°.
Если четырёхугольник можно вписать в окружность, то сумма противоположных углов этого четырёхугольника равна 180°.
⇒ ∠D = 180° - 82° = 98°.
AC = AB = 9 BC = 6 углы А=36, остальные по 72