
Противоположные углы параллелограмма равны. Углы, примыкающие к одной стороне - внутренние при пересечении параллельных прямых и секущей, их сумма равна 180°. ⇒
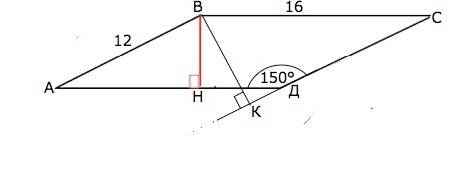
Угол ВАД=ВСД=180°-150°=30°.
Площадь параллелограмма равна произведению высоты на сторону, к которой проведена.
Высота ВН перпендикулярна стороне АД, ⇒∆ АВН - прямоугольный.
ВН противолежит углу 30° и равна половине гипотенузы АВ.
ВН=12:2=6 см.
S АВСД=ВН•АД=6•16=96 см²
Точно так же высота ВК, проведенная к СД, равна половине ВС, т.е. 8 см.
S АВСД=8•12=96 см²
Построим прямоугольный треугольник АВС в котором АС – гипотенуза равна 13, АВ – катет равен 12.
По теореме Пифагора найдем второй катет:
ВС= √(АС^2 –АВ^2)= √(13^2-12^2)= √(169-144)= √25=5
Формула площади прямоугольного треугольника: S=1/2 a*b (где a и b катеты треугольника)
Sabc=1/2*АВ*ВС=1/2*12*5=30 кв. ед.