
Объяснение:
1)
Если две плоскости имеют хотя
бы одну общую точку, то они пере
секаются и их пересечением явля
ется прямая (не рассматриваем ва
риант совпадения двух плоскостей).
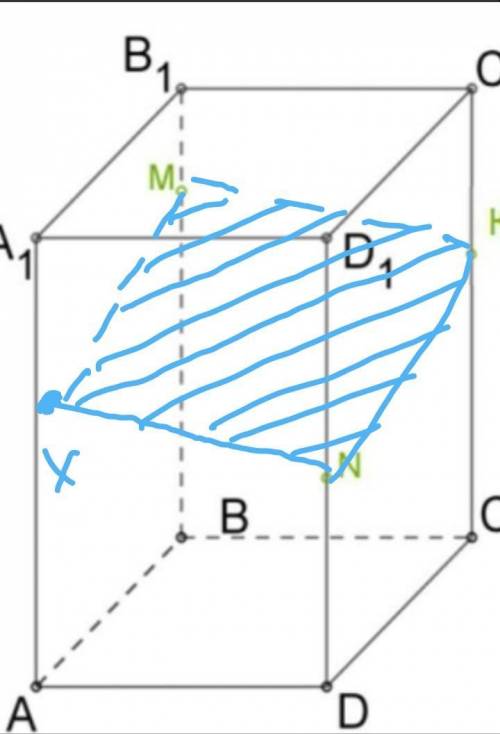
В данной ситуации плоскость сече
ния MKN будет пересекать все че
тыре вертикальные грани парал
лелепипеда.
2)
Если две параллельные плоскости
пересекает третья плоскость, то
прямые пересечения параллель
ны.
3)
В противоположных гранях че
рез данные точки проводим ( сое
диняем точки М и K ) прямую МK
и через точку N параллельно МK
прямую NX. Отрезки МK и NX яв
ляются линиями сечения;
(соединяем точки K и N) прово
дим прямую KN и через точку М
параллельно KN прямую МХ. От
резки KN и МХ являются линия
ми сечения.
4)
Искомое сечение - четырехуголь
ник МКNX, который является пря
моугольником.
(В общем случае ответ дает теорема Чевы (и Ван-Обеля), но в данном случае есть уникальная возможность сразу получить ответ.)
Я продлеваю сторону AB за точку B до точки D, так, что AB = BD; точку D я соединяю с вершиной C.
В треугольнике ADC BM - средняя линия, то есть BM II DC; кроме того, отрезок CB играет роль медианы. Поскольку BK:KC = 1:2; точка K - центроид треугольника ADC (ну, проще говоря, точка пересечения медиан). Поэтому AK - часть медианы ADC (при продолжении AK за точку K эта прямая разделит DC пополам в точке, которую я обозначу N).
Само собой, это означает, что AK делит пополам и BM (там подобные треугольники ANC и AOM, AND и AOB, и CN = ND => MO = OB).
Итак, точка O делит BM пополам.
(Кажется, я так длинно изложил, но "в голове" это всего один шажок).
Дальше все просто - из полученного следует, что от точки O до BC расстояние в 2 раза меньше, чем от точки M до BC. И BK = BC/3;
Поэтому площадь BOK равна (1/2)*(1/3) = 1/6 от площади BMC; (ну, высота к основанию меньше в 2 раза, а само основание - в 3, роль "основания" играют BC и BK)
а площадь BMC составляет 1/2 от площади ABC (аналогично предыдущему замечанию в скобках, только тут "основания" - AM и AC, а высота - расстояние от B до AС, в этом случае высота общая)
ответ 1/12