1)наидите углы которые образуют диагонали ромба с его сторонами если один из углов равен 45 градусов
пусть <В=45 град
тогда противоположнве углв попарно равны <D=<B=45
сумма односторонних углов = 180 град
<A+<B=180 , тогда <A=180-45=135, тогда <C=<A=135
диагонали ромба являются бисектриссами углов ромба, т е делят их пополам
<A /2=135/2=67,5 град = 67 град 30 мин
<C - также как А
<B/2 = 45/2=22,5 град = 22 град 30 мин
<D - также как В
2)наидите периметр ромба ABCD ,если <B=60градусов.AC=10.5см
у ромба все стороны равны
значит АВ=ВС
значит треуг АВС - равнобедренный (углы приосновании АС равны)
Тогда <A = <C = (180-<B)/2=(180-60)/2=60
то есть треугольник к тому же правильный
углы все 60 град -- а знчит и стороны все равны
АВ=ВС=АС=10.5см
у ромба все стороны равны
АВ=ВС=АС=10.5см=AD=DC
Периметр p=4*10.5=42см
ΔABC - равнобедренный;
высота BD = 6,4 см;
AB = BC = 12,8 см.
Найти:∠A = ?°; ∠B = ?°; ∠C = ?°.
Решение:Высота, проведённая к основанию равнобедренного треугольника, является и медианой, и биссектрисой.
⇒ AD = DC, ∠ABD = ∠BDC (по выше указанному свойству).
⇒ ΔABD = ΔCBD (по двум сторонам и углу между ними).
Нам также известно что равные треугольники прямоугольные (высота BD).
Если катет равен половине гипотенузы, то напротив лежащий угол составляет 30°.
Боковые стороны равнобедренного ΔABC - гипотенузы прямоугольных ΔABD и ΔСBD, а высота - общий катет.
Как мы уже отметили, этот общий катет равен половине гипотенузы, так как 6,4 * 2 = 12,8 см. Поэтому ∠A = ∠C = 30°.
Сумма острых углов в прямоугольном треугольнике равна 90°.
⇒ ∠ABD = ∠CBD = 90° - 30° = 60°. ⇒ ∠B = 120°.
ответ: ∠A = ∠C = 30°, ∠B = 120°.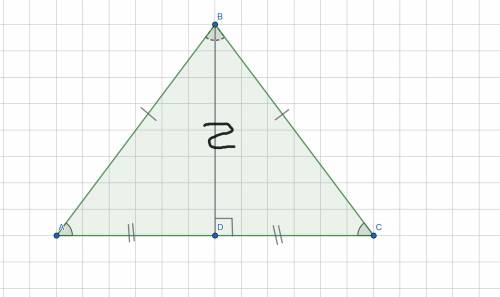
Начертить окружность, через центр окружности провести взаимноперпендикулярные прямые. Угол АОВ - прямой. От точки А отложить раствором циркуля (радиус тот же, что при проведении окружности) дугу на окружности. Полученная точка С образует угол СОВ=150 град.