Question

1)в треугольник hpt вписана окружность с центром a и радиусом, равным 7м. найдите длину отрезка ah, если угол pht равен 90 градусов. 2)в окружности с центром о вписан равнобедренный треугольник с основание аб=12 м, высота ch=2 м. найдите радиус окружности, если угол с-тупой

Answer 1

1. В прямоугольный треугольник вписана окружность (см. рис 1). Проведем радиусы AN и AM к катетам HP и HT соответственно. Как видно из рисунка, образовался квадрат HNAM, для которого отрезок AH является диагональю.
Диагональ квадрата найдем по формуле:
$d=a \sqrt{2}$, где d = AH - диагональ квадрата, a - сторона квадрата, которая нам известна (7м).
$AH=d=7 \sqrt{2}$
ответ: $7 \sqrt{2}$ .
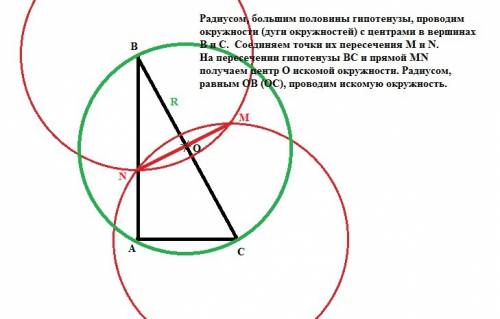
2. В окружность вписан равнобедренный треугольник с тупым углом (см рис. 2). Для нахождения радиуса описанной окружности воспользуемся формулой:
$R= \frac{abc}{4S}$, где a, b и c - стороны треугольника, а S - площадь треугольника.
Найдем площадь треугольника:
$S= \frac{1}{2}*CH*AB= \frac{1}{2}*12*3=18$;
Найдем сторону треугольника AC из ΔHCA (∠H = 90°):
$AC= \sqrt{ CH^{2}+ AH^{2} } = \sqrt{4+36} = \sqrt{40}=2 \sqrt{10}$
AC = BC, т. к. треугольник равнобедренный.
Найдем радиус окружности:
$R= \frac{AC*BC*AB}{4S} = \frac{2 \sqrt{10}*2 \sqrt{10} *12 }{4*18}= \frac{20}{3}$
ответ: $\frac{20}{3}$ м.