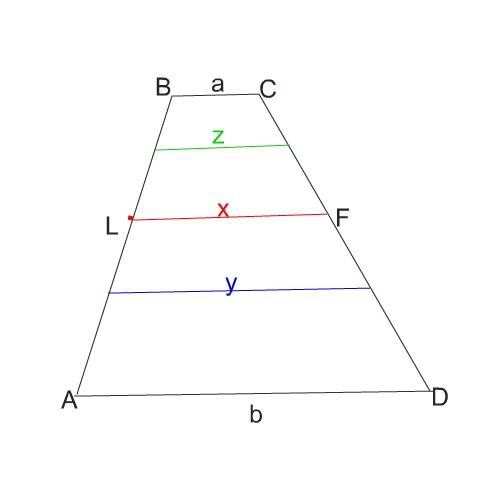
Обязательно смотрим рисунок.
И примем во внимание, что получающиеся трапеции подобны не исходной.
Если трапеции ALFD и LBCF подобны, то a/LF = LF/b.
Отсюда LF = √(ab).
Таким образом, отрезок разбивающий трапецию на две подобные трапеции, имеет длину равную среднему геометрическому длин оснований.
---
Делим трапецию:
1 отрезок между основаниями исходной:
х²=2*8=16
х=√16=4
Второй отрезок между первым и основанием исходной трапеции
у²=4*8=32
у =√32=4√2
Третий отрезок - идет под меньшим основанием
z²=2*4=8
z=2√2
---------------------------
Отрезки в рисунке идут в таком порядке
z, x, y
---------------
Коэффициент подобия между этими четырьмя трапециями попарно ( смежными) равен
4:2√2=2:√2=2√2:√2·√2=2√2:2=√2
k=√2
Площади подобных фигур относяся как квадрат коэффициента их подобия.
Для этих трапеций это
(√2)²=2
Площадь второй по величине относится к нижней -большей- как 1:2=1/2
Третьей ко второй 1/2:2=1/4
и последней
1/8
сложим площади
1/2+1/4+1/8 =( 4+2+1)/8=7/8
7/8 < 1
Площадь самой большой из этих четырёх трапеций больше суммы площадей остальных трёх
Утверждение В) верно, но только для прямых, лежащих в одной плоскости.
Объяснение:
Определение: "Две прямые, пересекающиеся под прямым углом, называются перпендикулярными" (для плоскости).
Определение: "Две прямые называются перпендикулярными, если угол между ними равен 90°". (для пространства). При этом они не имеют общей точки.
Утверждение А) не верно, так как отрезок по определению - часть прямой, ограниченная двумя точками. Отрезки, лежащие на перпендикулярных прямых, могут располагаться на участках этих прямых, не включающих точку пересечения.
Утверждение Б) не верно по этой же причине, так как луч - это часть прямой, имеющий начальную точку и его можно продолжить только в одну сторону. Лучи, лежащие на перпендикулярных прямых, могут располагаться на участках этих прямых, не включающих точку пересечения.
Утверждение В) верно, если прямые лежат в одной плоскости.
Утверждение Г) не верно по причине, указанной для утверждений А и Б.
h=(a+b)/2=(6+10)/2=8 см, S=(a+b)*h/2=(6+10)*8/2=64 см2