Сечением будет равнобедренная трапеция, т.к. основания призмы лежат в параллельных плоскостях, то секущая плоскость их будет пересекать по параллельным прямым.
Пусть К и М середины рёбер АС и ВС, тогда МК средняя линия, по свойству она параллельна третьей стороне АВ и равна её половине - 4 см (стороны основания равны по 8см)
Секущая плоскость проходит через точку А1 и параллельна МК, т.е. совпадает с А1В1 (МК II АВ II А1В1). А1В1МК - трапеция с основаниями А1В1=8см и МК=4см
Боковые стороны равны из равенства прямоугольных треугольников АА1К и ВВ1М (по двум катетам). А1К и В1М - гипотенузы этих треугольников. Их находим по теореме Пифагора √3²+4²=√9+16=√25=5см.
Р=4+8+2·5=22см
Задача на подобие треугольников.
Столб и человек по отношению к земле - перпендикулярны.
Если от вершины столба через голову человека провести прямую к концу его тени, получим подобные ( по общему острому углу) треугольники.
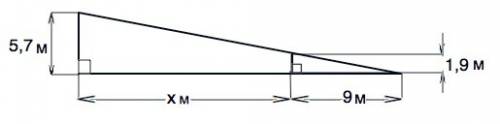
Высоту человека и столба примем за катеты прямоугольных треугольников, тень человека и расстояние от основания столба до конца тени человека - вторые катеты.
Длина тени столба равна сумме расстояния от его основания до человека и тени человека ( см. рисунок).
Сходственные стороны подобных треугольников пропорциональны. Составим пропорцию:
5,7:1,9=(х+9):9
5,7•9=1,9х+1,9•9
1,9х=9•(5,7-1,9)
1,9х=9•3,8
х=18 м- на таком расстоянии от столба стоит человек.
1) ВС=ВД+ДС=13,5+4,5=18 (см)
2) Р=АВ+АС+ВС=42, но ВС=18, значит АВ+АС=42-18=24 (см).
3) Пусть СА=х, тогда АВ=24-х. По свойству биссектрисы тр-ка: АВ/АС=13,5/4,5 или
(24-х)/х=13,5/4,5. Тогда по основному свойству пропорции: 7,5(24-х)=13,5х, значит
180-7,5х=13,5х или 180=21х. Т.е. х=180/24=7,5 (см) - сторона АС, а сторона АВ=
=24-7,5=16,5 (см).
ОТВЕТ: АВ=16,5 см, АС=7,5 см.