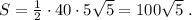Объяснение:
линейная ф-ция у=kх+b
прямая а имеет координаты (-2;0), (-1;2), подставляем в уравнение
первую точку 0= -2k+b b=2k
вторую точку 2= -k+b b=k+2
2к=к+2
к=2, b=2+2=4
значит уравнение прямой а выглядит как у=2х+2
прямая b имеет координаты (0;0), (-1;2), подставляем в уравнение
первую точку 0= 0*к+ b=0
вторую точку 2= -k+0 к= -2
значит уравнение прямой b выглядит как у= -2х
прямая с имеет координаты (-2;0), (2; -4), подставляем в уравнение
первую точку 0= -2k+b b=2k
вторую точку -4= 2k+b b= -4 - 2к
2к= -4 - 2к
4к= -4, к= -1 b= 2*(-1)= -2
значит уравнение прямой а выглядит как у= -х-2
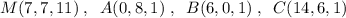
1) Высота правильной пирамиды проходит через СЕРЕДИНУ её основания. Основанием правильной четырёхугольной ПИРАМИДЫ служит КВАДРАТ. Его центр совпадает с точкой пересечения ДИАГОНАЛЕЙ, которая является СЕРЕДИНОЙ каждой из диагоналей квадрата.
Найдём координаты точки Н - середины ДИАГОНАЛИ АС:
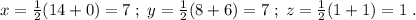
Итак, Н(7,7,1) .
Вычислим высоту МН пирамиды:
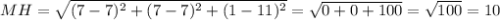
2) Апофема правильной пирамиды - это отрезок, соединяющий ВЕРШИНУ пирамиды с СЕРЕДИНОЙ стороны основания. Найдём координаты точки Р - середины СТОРОНЫ основания АВ:
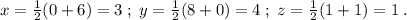
Итак, Р(3,4,1) . Следовательно,
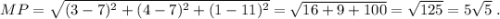
3) Площадь боковой поверхности правильной пирамиды равна ПОЛОВИНЕ произведения ПЕРИМЕТРА основания и апофемы пирамиды. Найдём сторону АВ - СТОРОНУ ОСНОВАНИЯ пирамиды:
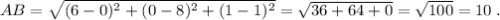
ВЫЧИСЛИМ ПЕРИМЕТР ПИРАМИДЫ: 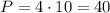 .
.
Вычислим площадь боковой поверхности пирамиды: