DE – радиус данной окружности.
Возьмём точку К (4;-7), проведем по линиям клеток DK и EK.
DK=|-5–(-7)|=|-5+7|=2
EK=|4–(-2)|=|4+2|=6
Так как углы любой клетки равны 90°, то угол DKE=90°.
Тогда по теореме Пифагора в ∆DKE:
DE²=DK²+EK²
DE²=2²+6²
DE²=4+36
DE²=40
То есть квадрат радиуса окружности равен 40.
Уравнение окружности имеет вид:
(x–a)²+(y–b)²=R²
где кординаты центра окружности (а;b), а R – радиус.
a) Центр окружности – точка D имеет кординаты (4;-5), тогда получим уравнение:
(x–4)²+(y+5)²=40
b) Центр окружности – точка E имеет кординаты (-2;-7), получим уравнение:
(х+2)²+(у+7)²=40
ответ выделен жирным шрифтом. Так как не дано какая из двух точек центр, я расписал два случая. Но вероятнее что всё-таки случай а)
Тогда ответ: (x–4)²+(y+5)²=40
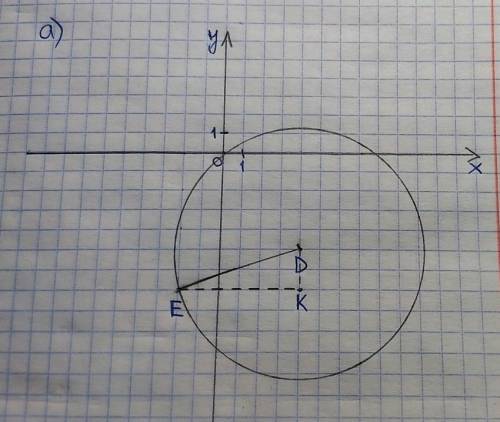
подобие
Sтрапеции = 1/2(AD + BC)h, где h - высота трапеции.
Пусть a1 = BC (меньшее основание), a2 = AD (большее основание), h1 - высота треугольника BOC, h2 - высота треугольника AOD (обе высоты проведены на из точки О).
Тогда Sтрапеции = 1/2(a1 + a2)(h1 + h2).
Угол CAD = углу BCA(как накрест лежащие углы при параллельных прямых BC и AD и секущей AC),
Угол DBC = углу ADC(как накрест лежащие углы при параллельных прямых BC и AD и секущей BD),
значит, ΔBOC подобен ΔDOA (по двум углам).
По теореме о соотношении площадей подобных треугольников
SΔAOD/SΔBOC = k^2 (k - коэффициент подобия).
SΔAOD/SΔBOC = 8/2 = 4 => k = 2.
Значит, a2/a1 = h2/h1 = 2.
h2 = 2h1, a2 = 2a1 => Sтрапеции = 1/2 * 3a1 * 3h1 = 3a1*h1.
SΔBOC = 1/2*a1*h1 = 2 => a1*h1 = 4.
Итак, Sтрапеции = 3*4 = 12.
В нашем случае P = 146,08 см, а площадь равна П*D/2*D/2, то есть 1698,23 см. Для более точных результатов есть калькулятор (думаю число Пи найдешь).