Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины треугольника.
Пусть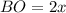 
см и 
см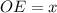, тогда 
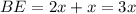, что по условию он равен 9 см.
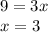
Следовательно,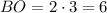 
см и 
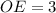см
Аналогично, пусть теперь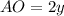 
см и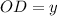 
, тогда 
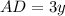и по условию равен 12 см
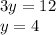
Таким образом,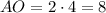 
см и 
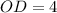см.
По условию медианы треугольника AD и BE взаимно перпендикулярны, следовательно
По теореме Пифагора из прямоугольного треугольника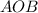 
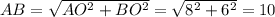см
По теореме Пифагора из прямоугольного треугольника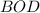 
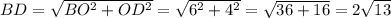см
Тогда 
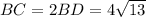см
Из прямоугольного треугольника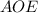 
по теореме Пифагора
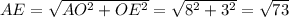см
Тогда 
см
ответ: 
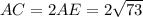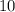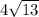см;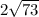 
см; 
см.
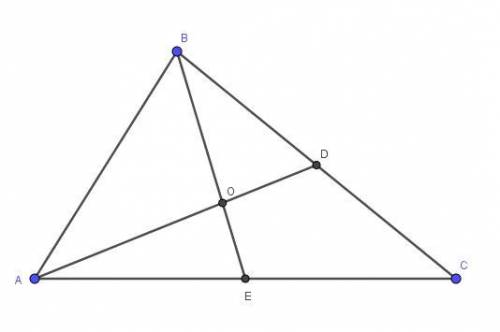
Пусть дан четырехугольник ABCD и AO=CO, BO=DO, где точка О - точка пересечения диагоналей АС и BD
Треугольники AOB и СOD равны за двумя сторонами и углом между ними,
AO=CO, OВ=OD,углы AOB и СOD равны как вертикальные
Треугольники AOD и COB равны за двумя сторонами и углом между ними,
AO=CO, OВ=OD,углы AOB и СOD равны как вертикальные
С равенства треугольников получаем равенство углов
угол BAC=уголDCA
уголDAC=уголBCA
з их равенства следует(они будут внутренними разносторонними)
что прямые AB и CD, AD и BC - паралельны,
а значит четырехугольник паралелограмм, доказано.
Расстояние от точки до прямой - это перпендикуляр из этой точки до прямой, и любая наклонная будет больше этого перпендикуляра.