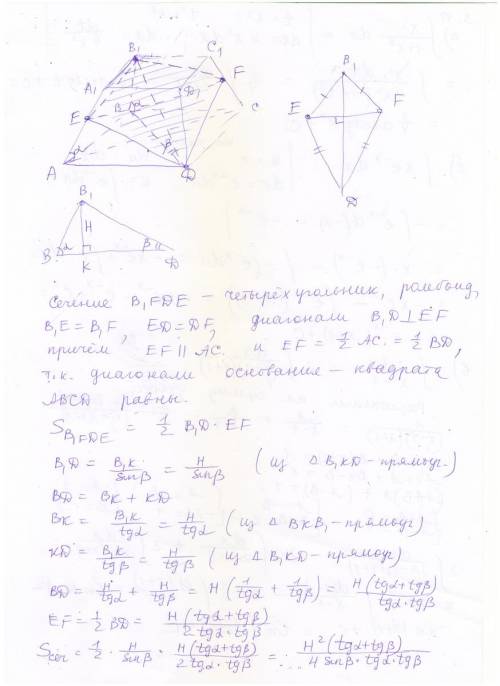
В равнобокой трапеции диагональ перпендикулярна боковой стороне и является биссектрисой острого угла при основании. Найти высоту трапеции , если ее площадь равна 9√3
Объяснение:
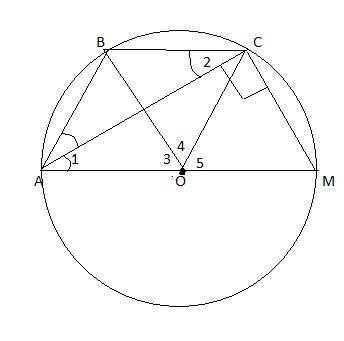
АВСМ-равнобедренная трапеция.
1)Если трапеция является равнобедренной, то около неё можно описать окружность. Пусть О-принадлежит АМ . Тогда ОА=ОС=ОМ как центры описанной окружности , т. к. центр описанной окружности лежит на середине гипотенузы .
2)Углы 1 и 2 равны как накрест лежащие при АМ||ВС, АС-секущая⇒ΔАВС-равнобедренный и ВА=ВС. Значит и ВА=ВС=МС.
3)ΔОАВ=ΔОВС=ΔОСМ по трем сторонам ВА=ВС=МС, остальные радиусы......Значит
- ∠3=∠4=∠5=180°:3=60°.
- их площади равны и S(ΔОСМ )=9√3:3=3√3.
3)В ΔОСМ ,∠СОМ=60° и ОС=ОМ ⇒ два других угла по 60°⇒этот треугольник равносторонний.
S( равност.тр)=(а²√3):4 .Найдем сторону треугольника (а²√3):4=3√3 или а²=12 , а=√12 .
Площадь можно найти иначе S( равност.тр)=1/2*а*h.
3√3=1/2*√12*h или h=3.
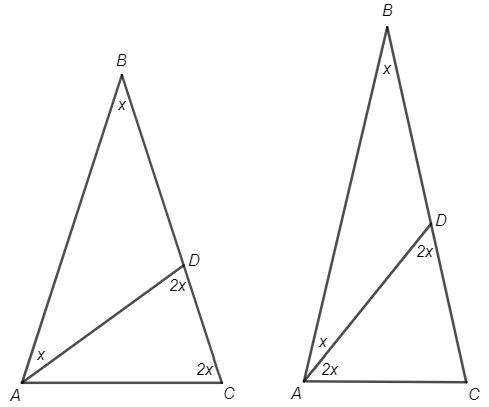
AC - основание равнобедренного △ABC.
Провели прямую AD.
В равнобедренном △ABD:
AD не является основанием, так как AB и BD не равны.
Предположим, что BD является основанием. Тогда ∠ADB - острый, смежный ∠ADC - тупой. В равнобедренном △ADC тупой угол может быть только против основания, но ∠DAC и ∠С не равны. Следовательно BD не является основанием.
Установили, что AB - основание равнобедренного △ABD.
Пусть B=BAD =x
Тогда ADC=2x (внешний угол)
В равнобедренном △ADC:
AC не является основанием, так как ∠DAC и ∠С не равны.
Возможны два случая:
1) DC является основанием
ADC=C=A =2x
A+B+C=180 => 5x=180 => x=36
B =36°
A=C =72°
2) AD является основанием
ADC=DAC=2x => A=C=3x
A+B+C=180 => 7x=180 => x=180/7
B =180°/7 ~25,71°
A=C =540°/7 ~77,14°