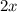 )
)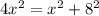
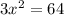
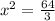
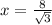
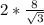 =
=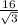
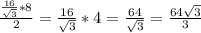 см²
см²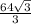 см²
см²
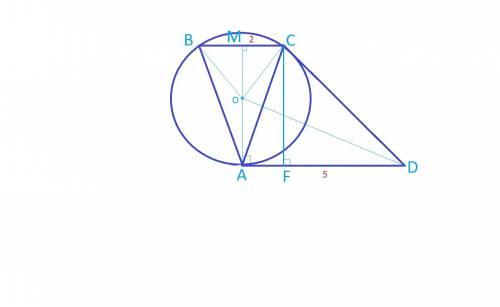
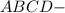 трапеция
трапеция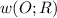 - описана около Δ
- описана около Δ 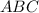
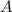 и
и 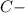 точки касания
точки касания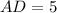
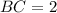
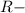 ?
?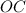 ⊥
⊥ 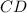
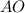 ⊥
⊥ 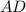
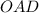 и Δ
и Δ 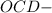 прямоугольные
прямоугольные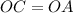 ( как радиусы)
( как радиусы)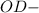 общая
общая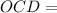 Δ
Δ 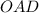 (по гипотенузе и острому углу)
(по гипотенузе и острому углу)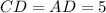
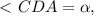 тогда
тогда 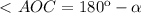
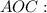
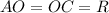

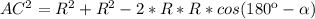
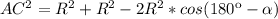
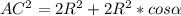
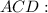


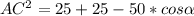
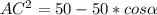
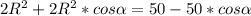
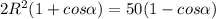
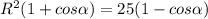
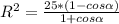
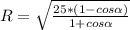 (1)
(1)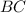 ║
║ 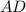
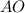 ⊥
⊥ 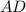
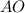 ∩
∩ 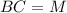 ⇒
⇒ 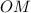 ⊥
⊥ 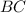
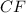 ⊥
⊥ 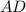
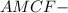 прямоугольник
прямоугольник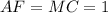
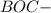 равнобедренный, значит
равнобедренный, значит 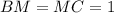
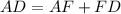
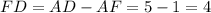
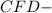 прямоугольный
прямоугольный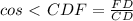
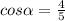
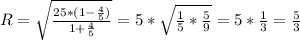
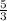
20^2 = 12^2 + h^2
h^2 = 20^2 - 12^2 = 400 - 144 = 256
h = 16
Sбок = 2*π*6*16 = 192π ~ 603,19 см^2
V = π*6^2*16 = 576π ~ 1809,6 см^3