1) центральным углом в окружности называется плоский угол с вершиной в её центре.
2) дуга
3) ∪
4) когда дуга принадлежит центральному углу
5) 360°
6) центральный угол равен дуге, на которую он опирается
7) хорда стягивает 2 дуги и их градусная мера равно 360°
8) угол вершина которого лежит на окружности, а стороны пересекают окружность
9) в том случае если она лежит внутри угла
10) градусная мера врисанного угла равна половине дуги, на которую он опирается.
11) выписаные углы опирающиеся на одну и ту же дугу - равны.
12) прямой
58 см
Объяснение:
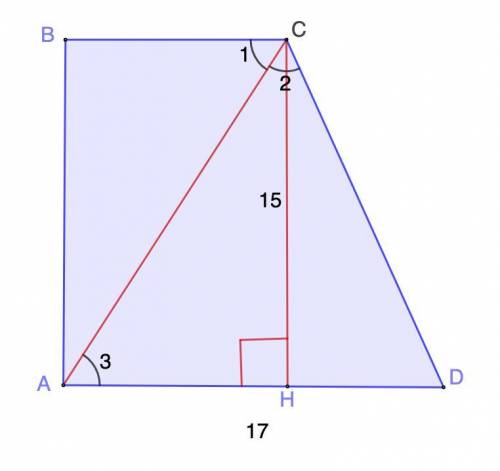
Дано: ABCD - прямоугольная трапеция.
АС - биссектриса;
СН = 15 см - высота;
AD = 17 см.
Найти: Периметр ABCD
1. Рассмотрим Δ ACD.
∠1 = ∠2 (АС - биссектриса)
∠1 = ∠3 (накрест лежащие при AD || BC и секущей АС)
⇒ ∠2 = ∠3
Если у треугольника два угла равны, то этот треугольник — равнобедренный.⇒ ΔACD - равнобедренный.
⇒ AD = DC = 17 см
2. Рассмотрим ΔHCD - прямоугольный.
По теореме Пифагора:
HD² = CD² - HC²
HD² = 289 - 225 = 64
HD = √64 = 8 (см)
3. Рассмотрим ABCD.
AB = CH = 15 см
ВС = АН = 17 - 8 = 9 (см)
Периметр - сумма длин всех сторон.⇒ Р = AB + BC + CD + AD = 15 + 9 + 17 + 17 = 58 (см)
По Теореме о сумме углов треугольника ( угол A + угол B + угол C = 180 градусов) =>
Пусть x = угол при основании, тогда
x + x + x - 18 = 180 гр-ов
3x= 180+18
3x=198
x=198/3
x=66
Все углы при основании равны 66 гр-ам т.к. треугольник равнобедренный
а вершина треугольника равна x-18 = 66-18=48
ответ: углы при основании = 66 гр-ов, вершина тр-ка равна 48 гр-ам