1). Когда мы нарисуем рисунок, то увидим, что это сечная. Отсюда ми уже знаем, что каждий противоположный внутренний угол будет равен противоположеному внутренему улу, така само и со внешнеми углами. Если взять только одну прямую с сечной, то это образуеться вертикальние углы, вместе с их особеностями.
Два сумежных угла будут равны 180гр., отсюда можно зделать вывод, что 80градусам може доривнювати только сума одинаковых углов., отсюда угол 6+угол3=80гр. Так, как углы равны, то угол 3=40гр. Теперь мы можем узнать, скольким градусам равен угол 4: 180-40=140гр.
ответ:1=140; 2=40; 3=40; 4=140; 5=140; 6=40; 7=40; 8=140гр.
2). Так, как треугольник равнобедренный значит и углы при основании будут равны, они становлять 75градусов.
Из треугольника АДС: угол АДС=90, так как это угол при высоте; Угол ДСА=75гр., отсюда угол ДАС=15гр.
ответ:15гр.
Если что то непонятно, спрашивай)))
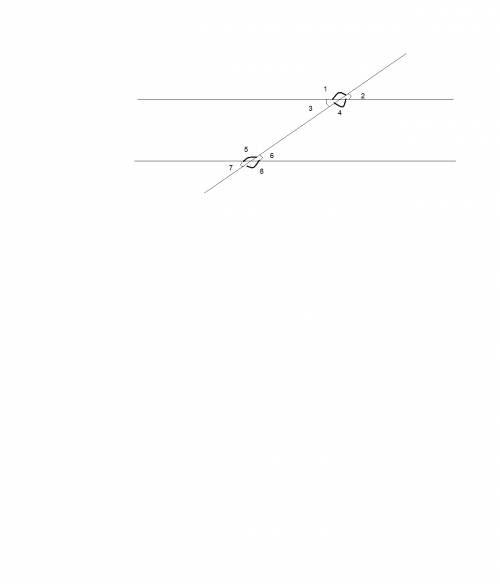
1). Когда мы нарисуем рисунок, то увидим, что это сечная. Отсюда ми уже знаем, что каждий противоположный внутренний угол будет равен противоположеному внутренему улу, така само и со внешнеми углами. Если взять только одну прямую с сечной, то это образуеться вертикальние углы, вместе с их особеностями.
Два сумежных угла будут равны 180гр., отсюда можно зделать вывод, что 80градусам може доривнювати только сума одинаковых углов., отсюда угол 6+угол3=80гр. Так, как углы равны, то угол 3=40гр. Теперь мы можем узнать, скольким градусам равен угол 4: 180-40=140гр.
ответ:1=140; 2=40; 3=40; 4=140; 5=140; 6=40; 7=40; 8=140гр.
2). Так, как треугольник равнобедренный значит и углы при основании будут равны, они становлять 75градусов.
Из треугольника АДС: угол АДС=90, так как это угол при высоте; Угол ДСА=75гр., отсюда угол ДАС=15гр.
ответ:15гр.
Если что то непонятно, спрашивай)))

Теперь представим сумму трех углов - это прибавляют два равных угла и один, смежный с ними. А затем, сравнивая эту сумму с четвертым углом, отнимают такой же смежный угол. Получается, что остается сумма двух равных углов, и она равна 240°.
∠1 + ∠2 +∠3 - ∠4 = 240°
Пусть равными будут ∠1 и ∠2, ∠3 и ∠4. Сделаем замены в равенстве.
∠1 + ∠1 + ∠3 - ∠3 = 240°
2 ∠1 = 240°
∠1 = 240° : 2 = 60°
∠2 = 60°
∠3 = 180° - 60° = 120°
∠4 = ∠3 = 120°
ответ. 60°, 60°, 120°, 120°