оТВЕТ ПИШЕТЕ ВЕРНЫЙ. ДЕЙСТВИТЕЛЬНО. ИСХОДНОЕ положение линейки подчиняется теореме ПИфагора. т.е. есть гипотенуза=20, есть катет=12, находим второй катет
√(20²-12²)=√((20-12)(20+12))=√(8*32)=√(4*64)=2*8=16.
Меняем теперь положение линейки, опуская ее верх на 1см. Теперь линейка-ка то осталась той же длины, т.е. 20см, а другой катет изменился 16-1=15, и новый ответ найдем так √(20²-15²) -12=
√((20-15)*(20+15)) -12=√(5*35)-12=5√7-12
ответ В) 5√7-12
Объяснение: №1. а₃=6√3, ⇒ r = а₃/2√√3 = 6√3 /2√√3= 3, a₆=r=3, ⇒ P₆=3·6=16, S₃ = a₃²√3/4 = 108√√3/4 = 28√3 №2. a₄ = 5√3, но а₄ =R√2, ⇒ R= 5√3/√2 = 5√6/4; ⇒А₄=2Rtg45°=2R = 5√6/2; ⇒ p₄= 4·5√3= 20√√3, P₄= 4·5√6/2 = 10√6; s₄= (5√3)²= 75, S₄= (5√6/2)²=37,5 №3. a₃= 3√5, ⇒ R = a₃/√3= 3√5/√3 = √15; a₆= 2Rtg(180°/6) = 2√15· √3/3= 2√√5; P₆= 6·2√5 =12√5; S₃= а₃²√3/4 = (3√5)²·√3/4 = 45√3/4
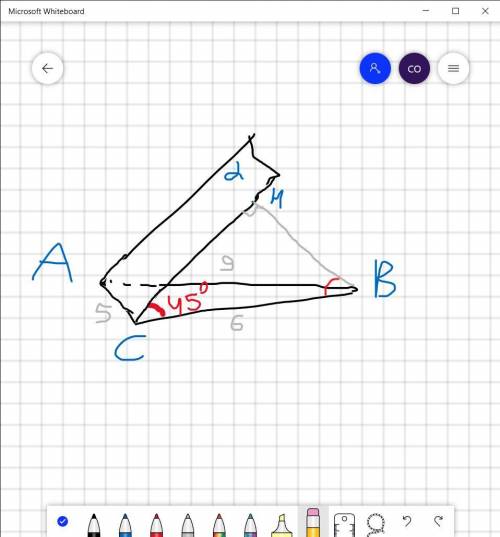
Дано: ΔABC
<(α,ABC)=45°
AB=9см ;BC = 6 см; AC = 5 см
α∩ABC =AC
BH⊥α
Знайти: BH
Розв'язання
ВС-похила до площини α, а ВН-перпендикуляр (оскільки відстань від точки до площини це перпендикуляр проведений із неї до цієї площини), тоді НС-проєкція.
Отже, проєкція похилої НС до площини трикутника ΔABC лежить на відрізку СВ => <HCB=<(α,ABC)=45°
Отримуємо прямокутний трикутник ΔВНС із прямим кутом <СНВ.
Знайдемо невідомий кут <НВС=90°-<HCB=90°-45°=45°
<HCB=<НВС, отже трикутник ΔВНС рівнобедрений і позначимо рівні сторони НС=НВ=х
За теоремою Піфагора
НС²+НВ²=СВ²
х²+х²=6²
2х²=36 | : 2
x²=18
x₁= -√18 (сторонній корень)
х₂=√18=√(9*2)=3√2 см
Відповідь: 3√2 см
(сподіваюся, що правильно)
теорема Пифагора================================