D = 100°,
A = B + 23°, B = A - 23°,
3 × A = C.
Сумма углов четырёхугольника равна 360°.
А + B + C + D = (B + 23°) + (A - 23°) + 3A + 100° = B + 23° + A - 23° + 3A + 100° = B + 4A + 100° = 360°;
B + 4A + 100° = 360°;
B + 4A = 360° - 100° = 260°;
A - 23° + 4A = 260°;
5A = 283°;
A = 56,6°;
B = A - 23° = 56,6° - 23° = 33,6°;
C = 3 × A = 3 × 56,6° = 169,8°.
ответ: А = 56,6°; В = 33,6°; C = 169,8°; D = 100°.
Проверим.
А + B + C + D = 56,6° + 33,6° + 169,8° + 100° = 360°;
A на 23° больше В, 56,6° на 23° больше 33,6°;
А в три раза меньше С, 56,6° в три раза меньше 169,8°.
Всё верно.
1.
Пусть дан ABCD - прямоугольник, SАВСD = 15 см, АВ = 5 см.
Найдём ВС - ?
По формуле для Sпрямоуг = a×b ⇒ Sпрямоуг = AB×BC
BC=Sпрямоуг /AB
ВС=15/5 = 3 см
ответ : ВС = 3 см
2.
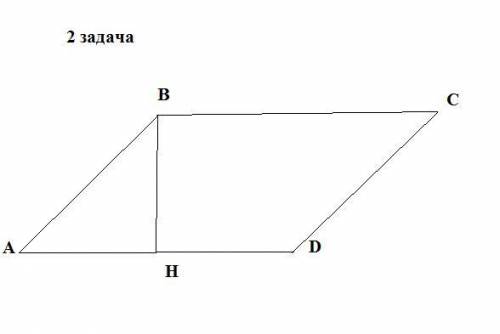
Пусть дан параллелограмм ABCD,∠В= 150°, две стороны 12 и 16 см. Найдём SABCD -?
Из вершины В проведём высоту ВН к стороне АД.
∠А = 180° - ∠В = 180° - 150° = 30°.
Рассмотрим △АВН : ВН является высотой и катетом и находится против ∠30°.
АВ-гипотенуза , значит ВН = АВ : 2 = 12 : 2 = 6 см.
SABCD = ВН × АД = 6 × 16 = 96 см².
ответ : SABCD = 96 см²
3.
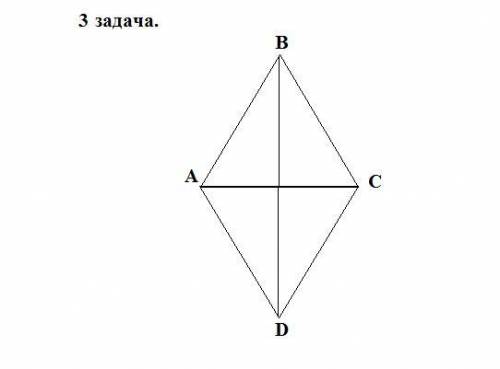
Пусть дан ромб АВСD , АС- диагональ , ∠АСD = 35° .Найдём ∠АВС - ?
АС - биссектриса, ∠АСD = ∠ВАС = 35°, как накрестлежащие.
Рассмотрим △АВС : равобедренный, т.к у ромба все стороны равны, значит углы при основании равны.
∠АВС=180° - 35° - 35° = 110°
ответ : 110°
4.
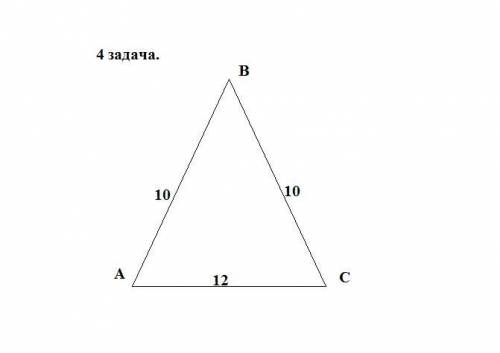
Пусть дан △АВС-равнобедренный , АС-основание = 12 см.
АВ=ВС=10 см. Найдём S△АВС-?
Рассмотрим △АВС : Проведем высоту ВН , △АВС-равнобедренный ⇒ ВН является высотой , медианой и биссектрисой. Образован прямоугольный треугольник АВН, АН = НС = 12/2 = 6 см.
По теореме Пифагора найдём катет ВН :
ВН=√АВ² - АН²
ВН=√64
ВН=8 см
S△АВС=(ВН×АС)/2
S=(8×12)/2
S=48 кв. см
ответ:48 кв.см.
6.
2,4

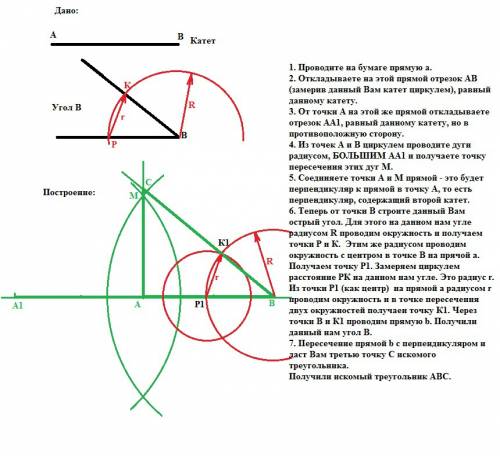
У тебя данных нет, поэтому построение по каким-то данным тебя должно устроить. Если что не ясно, спрашивай.
И еще не торопите меня. Я пришел из школы и даже мне делал уроки, накопилось много вопросов, адресованных лично мне