Question

Длина отрезка VB равна 8√3 м. Он пересекает плоскость в точке O. Расстояние от концов отрезка до плоскости соответственно равны 3 м и 9 м. Найди острый угол, который образует отрезок VB с плоскостью. Отрезок с плоскостью образует угол - ?
Отрезок VB точкой O делится на отрезки
?√3 м и ?√3 м

Answer 1

60°

2√3

6√3

Объяснение:

Расстояние от концов отрезка до плоскости - это перпендикуляры:

Проведём VA⊥ плоскости ⇒VA⊥ОА.

Аналогично ВС⊥СО.

Получили прямоугольные треугольники: ΔVАО и ΔВСО

Пусть VО = х м, тогда ВО = (8√3-х) м

∠VОА=∠ВОА - как вертикальные. Обозначим их α.

ΔVАО: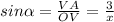     $sin\alpha =\frac{VA}{OV} =\frac{3}{x}$

ΔВСО: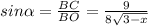     $sin \alpha =\frac{BC}{BO} =\frac{9}{8\sqrt{3-x} }$

$\frac{3}{x} =\frac{9}{8\sqrt{3-x} }$

$24\sqrt{3} -3x=9x$

$12x=24\sqrt{3}$

$x=2\sqrt{3}$

VО = 2√3 м, тогда ВО = 8√3-2√3=6√3 м

$sin \alpha =\frac{3}{2\sqrt{3} } =\frac{\sqrt{3} }{2}$

∠α = 60°