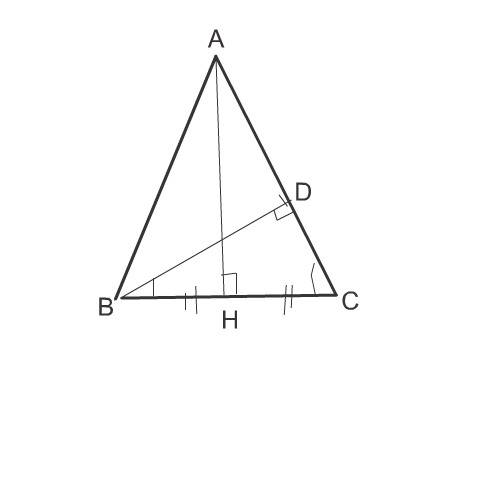
Треугольник АВС с основанием ВС - равнобедренный.
Из вершины А этого треугольника опустим высоту АН на основание ВС
Т.к. треугольник равобедренный, эта высота, являясь и медианой, делит основание ВС на две равные части.
Рассмотрим треугольники АНС и ВDС.
Они подобны, так как угол С в них общий, а прямоугольные треугольники с равным острым углом подобны.
ВD:АН=DC:НС
Из прямоугольного треугольника ВDС найдем катет DC по теоеме Пифагора
СD²=ВС²- DB²
СD²=900-576=324
СD=18
ВD:АН=DC:НС
24:АН=18:15
18 АН=360
АН=20
Площадь АВС=АН*НС
S АВС=20*15=300 см²
Сначала нужно найти АС и СВ (Так как это катеты соответственно прилежащий и противолежащий углу А) по Теореме Пифагора: (3х)^2+(5x)^2=34^2; 9x^2+25x^2=34^2. Значит, 34х^2 = 34^2. Значит единица измерения сторон треугольника равна \sqrt{34}.
Аналогично найдем, единицу измерения треугольника АСH (3y)^2+(5y)^2=(5sqrt{34})^2
9y^2+25y^2=25*34; 34y^2=25*34; y^2=25; y=5. CH=3y, AH = 5y (Так как это катеты соответственно противолежащий и прилежащий углу А),то CH=15, AH=25. Так как HB = AB - AH, то HB = 34 - 25 = 9.
ответ: BH = 9.
Поскольку АД∈АМД, ДМ∈АМД и СД∈СДМ, ДМ∈СДМ, то ∠АДС - это угол между плоскостями АМД и СДМ.
Диагонали пересекаются в точке О. АО=ОС=8 см, ВО=ОД=6 см.
В тр-ке АОД tg(АДО)=АО/ОД=8/6=4/3.
∠АДС=2arctg4/3≈2·53.13°≈106.26° - это ответ.