AC₁=2
AD₁=√5
Объяснение:
1. Рассмотрим ΔАВС (см. рис. 1). Он равнобедренный с АВ=ВС=1 и ∠В=120° (как внутренний угол правильного шестиугольника). Опустим высоту ВО на АС. Получили два равных прямоугольных ΔАВО = ΔСВО с углами 60°, 30° и 90° (т.к. ВО в равнобедренном тр-ке есть биссектрисой).
По теореме Пифагора,
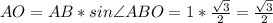
тогда АС=АО*2=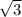
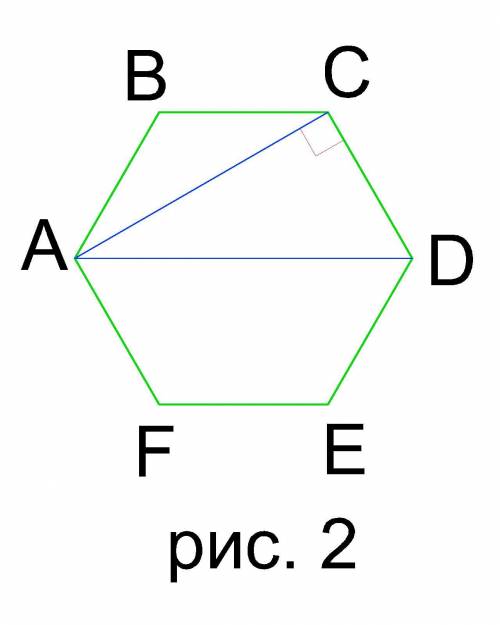
Рассмотрим ΔACC₁ (см. рис. 3). Он прямоугольный с двумя известными катетами
АС=√3, CC₁=1. Гипотенуза АС₁ является искомой величиной.
По теореме Пифагора: 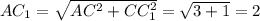
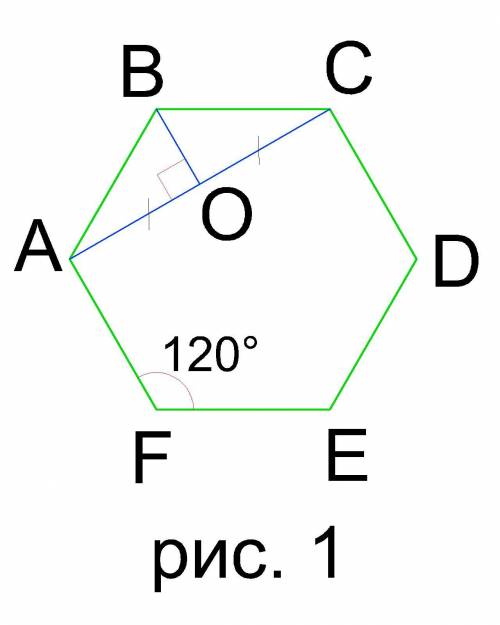
2. Рассмотрим ΔACD. Он прямоугольный с двумя известными катетами
АС=√3, CD=1 (см. рис. 2). Найдем гипотенузу АD.
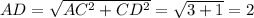
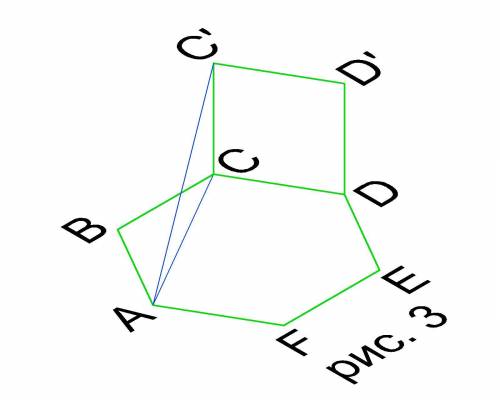
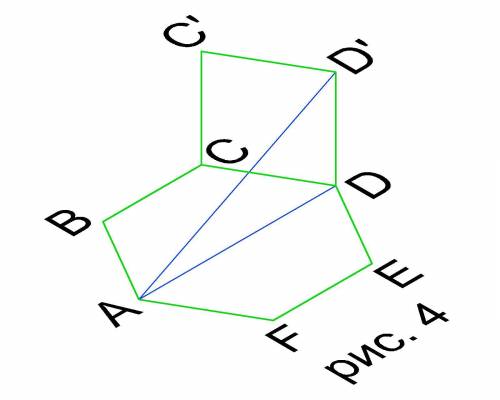
Рассмотрим ΔADD₁ (см. рис. 4). Он прямоугольный с двумя известными катетами
АD=2, DD₁=1. Гипотенуза АD₁ является искомой величиной.
По теореме Пифагора: 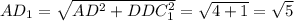
ABCK - трапеция, ∠A = ∠B = 90°,
CK=3см, ∠K=45°,
CH⊥AK, AH=HK=
Найти:
Решение:
HK = CK·cos ∠K = 3·
∠HCK = 90°-45°=45°, т.е. ΔHCK - равнобедренный ⇒СH = HK
ответ: 6,75 см².
2)Дано:
ABCK - трапеция, ∠С = ∠D = 90°,
AB=8 см, ∠A=60°,
BH⊥AD, AH=HD=
Найти:
Решение:
AH = AB·cos ∠A = 8 · cos 60° = 8 ·
BH = AB·sin ∠A = 8 · sin 60° = 8 ·
ответ: площадь трапеции равна 24√3 см².