так как треугольник равнобедренный следовательно две его боковые стороны равны.
Составим уравнение
3Х+3Х+Х=70
7Х=70
основание Х = 10
каждая боковая сторона 3*Х=30
Теорема о 30-градусном угле такова: Катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы.
Тоесть катет BC — равен половине гипотенузы AB.
Но нам эта информация не в решении задачи, продолжим.
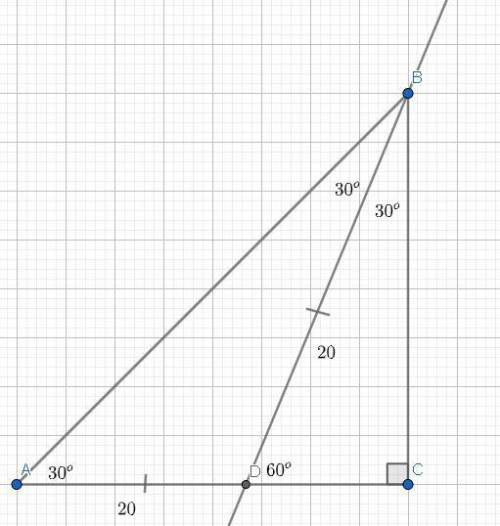
<B = <C - <A = 90-30 = 60°.
BD биссектриса — делит угол B — пополам, тоесть: <ABC == <DBC = 60/2 = 30°.
<A == <ABD = 30° => AD == DB; треугольник ABD — равнобедренный.
BD = 20 => AD == BD = 20.
<BDC = 30° => DC = DB/2 (теорема о 30-градусном угле прямоугольного треугольника).
DB = 20 => DC = 20/2 = 10
AD = 20; DC = 10 => AC = 10+20 = 30.
Вывод: AC = 30.
ΔАВС, АВ=ВС=зх,АС=х. АВ+ВС+АС=Р, 3х+3х+х=70, 7х=70, х=10.
АС=10, АВ=ВС=3·10=30.
ответ:10см. 30см, 30см.