r = 6 см
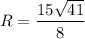 см
см
Объяснение:
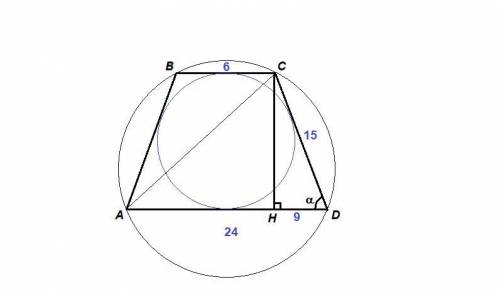
Трапеция вписана в окружность, значит она равнобедренная.
AB = CD.
Трапеция описана около окружности, значит суммы противоположных сторон равны.
AB + CD = AD + BC = 24 + 6 = 30 см
AB = CD = 30 : 2 = 15 см
Проведем высоту СН.
По свойству равнобедренной трапеции отрезок HD равен полуразности оснований:
HD = 0,5 · (AD - BC) = 0,5 · (24 - 6) = 0,5 · 18 = 9 см
ΔCHD: ∠CHD = 90°, по теореме Пифагора
CH = √(CD² - HD²) = √(15² - 9²) = √(225 - 81) = √144 = 12 см
Радиус окружности, вписанной в трапецию, равен половине ее высоты.r = 0,5 CH = 0,5 · 12 = 6 см
ΔCHD: ∠CHD = 90°
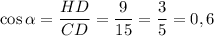
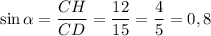
Из ΔACD по теореме косинусов:
AC² = AD² + CD² - 2 · AD · CD · cosα
AC² = 24² + 15² - 2 · 24 · 15 · 0,6
AC² = 576 + 225 - 432 = 369
AC = √369 = 3√41 см
Треугольник ACD вписан в ту же окружность, что и трапеция.
По следствию из теоремы синусов:

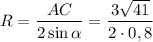
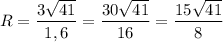 см
см
Объяснение:
8.
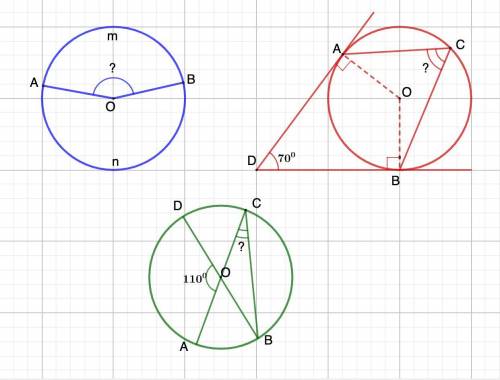
Дано: Окр.О;
∪AmB : ∪AnB = 9 : 11
Найти: ∠АОВ
Вся окружность - 360°.
Пусть ∪AmB = 9x, тогда ∪AnB = 11x.
Составим уравнение:
9х + 11х = 360°
20х = 360°
х = 18°
⇒ ∪АmB = 18°·9 = 162°
Центральный угол равен градусной мере дуги, на которую он опирается.⇒ ∠АОВ = 162° (центральный).
9.
Дано: ∠D = 70°
Окр.О - вписанная;
Найти: ∠АСВ
Рассмотрим DACB.
Радиус, проведенный в точку касания, перпендикулярен касательной.⇒ ∠DAO = ∠OBD = 90°
Сумма углов четырехугольника равна 360°.⇒ ∠АОВ = 360° - ( 70° + 90° + 90°) = 110°
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.⇒ ∠АСВ = ∠АОВ : 2 = 110° : 2 = 55° (вписанный)
10.
Дано: Окр.О
АС и ВD - диаметры.
∠AOD = 110° - центральный.
Найти: ∠АСВ
Центральный угол равен градусной мере дуги, на которую он опирается.⇒ ∪AD = ∠AOD = 110°
Диаметр делит окружность на две полуокружности.⇒ ∪DAB = 180°
∪AB = 180° - ∪AD = 180° - 110° = 70°
Вписанный угол равен половине градусной меры дуги, на которую он опирается.⇒ ∠ACB = ∪AB : 2 = 70° : 2 = 35°