m = 2c+3a
2c = 2*(-1:0) = (-2;0)
3a = 3*(1;2) = (3;6)
m = (-2;0)+(3;6) = (1;6)
ответ : (1;6)
Объяснение:
Дано:
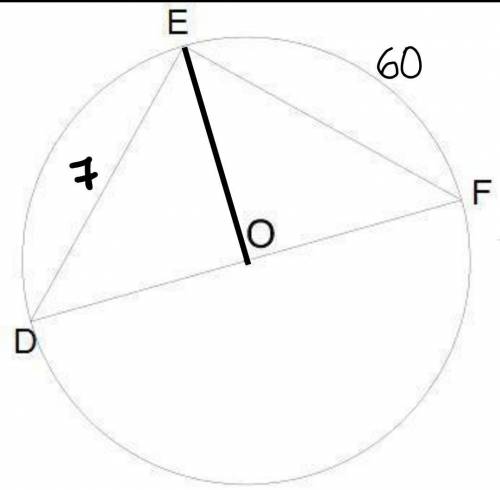
Окружность с центром в точке О;
Дуга ED=60°;
ED=7 см.
Найти: длину окружности.
Проведем ЕО.
Угол ЕОF – центральный и опирается на дугу EF, тогда угол EOF=дуга EF=60°.
Угол DOE=180°–угол EOF=180°–60°=120° (смежные углы)
DO=EO так как радиусы равны, следовательно ∆ЕОD – равнобедренный с основанием ED.
Углы при основании равнобедренного треугольника равны, тогда угол DEO=угол ODE=(180°–угол DOE)÷2=(180°–120°)÷2=60°÷2=30°.
По теореме синусов в ∆EOD:
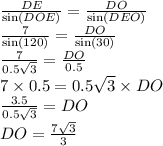
DO – радиус окружности.
C=2πr, где С – длина окружности; r – радиус окружности.
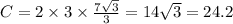
ответ: 24,2 см.
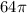см³.
Обозначим данную пирамиду буквами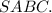 
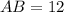см.
Проведём высоту пирамиды SO.
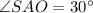
Начертим около этой пирамиды конус.
Так как конус описан около данной пирамиды, то высота конуса совпадает с высотой данной пирамиды.
=======================================================
Так как данная пирамида - правильная, треугольная ⇒ основание данной пирамиды - правильный треугольник.
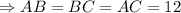см.
Проведём высоту 
в 
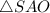- прямоугольный, так как 
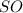- высота пирамиды.
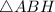- прямоугольный, так как - высота .
Так как - равносторонний ⇒ - высота, медиана и биссектриса
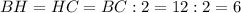см, так как - медиана.
Найдём по теореме Пифагора 
.
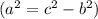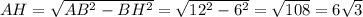см.
Точка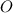 
- пересечение медиан и делит их в отношении 
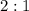, считая от вершины.
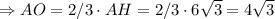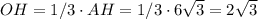см
см.
Также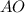 
- радиус описанной около окружности.
Рассмотрим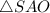
Если угол в прямоугольном треугольнике равен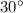 
, то напротив лежащий катет равен половине гипотенузы.
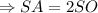
Составим уравнение:
Пусть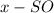 
, тогда 
.
И по теореме Пифагора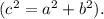 
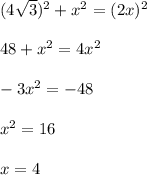
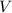конуса = 
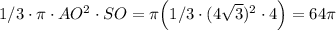см³.
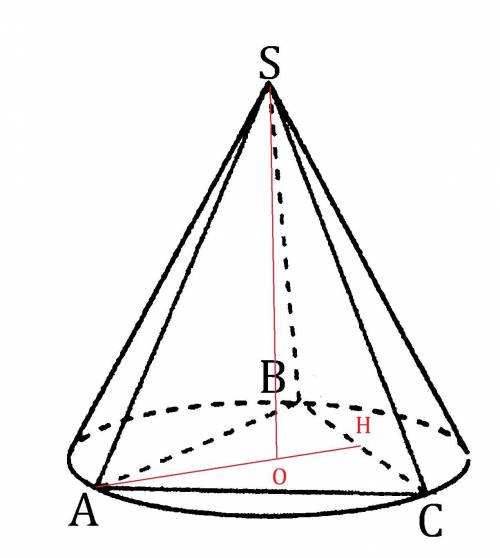
решение представлено на фото