Биссектрисы двух внешних углов и внутреннего угла треугольника пересекаются в центре вневписанной окружности.
Центр вписанной окружности треугольника (I) является точкой пересечения биссектрис, AI - биссектриса ∠BAC
△BAI=△DAI (по двум сторонам и углу между ними)
∠BIF=∠DIF (смежные с равными)
AF - биссектриса внешнего угла ∠BID треугольника BEI
EF - биссектриса внутреннего угла ∠BEI
F - центр вневписанной окружности △BEI
BA - биссектриса внутреннего угла ∠EBI треугольника BEI
A - центр вневписанной окружности △BEI
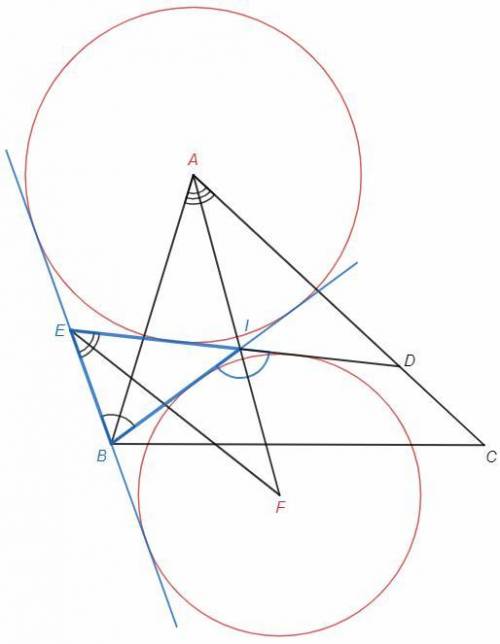
Биссектрисы двух внешних углов и внутреннего угла треугольника пересекаются в центре вневписанной окружности.
Центр вписанной окружности треугольника (I) является точкой пересечения биссектрис, AI - биссектриса ∠BAC
△BAI=△DAI (по двум сторонам и углу между ними)
∠BIF=∠DIF (смежные с равными)
AF - биссектриса внешнего угла ∠BID треугольника BEI
EF - биссектриса внутреннего угла ∠BEI
F - центр вневписанной окружности △BEI
BA - биссектриса внутреннего угла ∠EBI треугольника BEI
A - центр вневписанной окружности △BEI

искомый угол ---угол HKF
найдем FH: треугольник FHC прямоугольный, угол HCF = 45 град., FC=2 => HF = FC*sin45 = 2*корень(2)/2 = корень(2)
найдем КF: треугольник ОКF прямоугольный, ОF=2 => КF = корень(4+4) = 2*корень(2)
sin(HKF) = HF/KF = корень(2) / 2*корень(2) = 1/2
угол HKF = 30 град.
2))) чтобы построить сечение, перпендикулярное ADC1, нужно провести перпендикуляр из K к DC1 и продолжить его до пересечения с DD1 (H), получится треугольник EKH
DK = DH, т.е. KH соединяет середины сторон квадрата DD1C1C, EK соединяет середины сторон квадрата, получившийся треугольник EKH равносторонний
найдем EK: EK = корень(2)
Периметр P = 3корень(2)