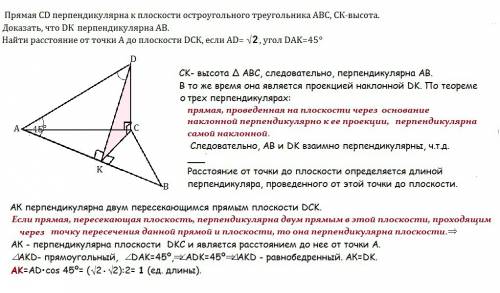
СK- высота ∆ АВС, следовательно, перпендикулярна АВ.
В то же время она является проекцией наклонной DK. По теореме о трех перпендикулярах:
прямая, проведенная на плоскости через основание наклонной перпендикулярно к ее проекции, перпендикулярна самой наклонной. Следовательно, АВ и DK взаимно перпендикулярны, ч.т.д.
___
Расстояние от точки до плоскости определяется длиной перпендикуляра, проведенного от этой точки до плоскости.
АК перпендикулярна двум пересекающимся прямым плоскости DCK.
Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.⇒
АК - перпендикулярна плоскости DKC и является расстоянием до нее от точки А.
⊿ АKD- прямоугольный, ∠ DAK=45º,⇒∠ ADK=45º⇒
⊿ АKD - равнобедренный. АК=DK.
AK=AD•cos 45º= ( √2•√2):2=1 (ед. длины).
в-боковые стороны треугольника
а-основание
R-радиус
h-высота
S-площадь треугольника
в=с, так как треугольник равнобедренный
C=2πR
50π=2πR
R=50π/2π=25
S=aвc/4R=aв²/4R
S=ah/2
aв²/4R=ah/2 | *4R
aв²=2Rah
в²=2Rah/a=2Rh=2*25*32=1600
в=√1600=40
(а/2)²=в²-h²=(в-h)(в+h)=(40-32)(40-32)=8*72=8*8*9
a/2=√8*8*9=8*3=24
a=24*2=48
P=a+в+с=а+в+в=а+2в=48+2*40=48+80=128
отв: 128 см