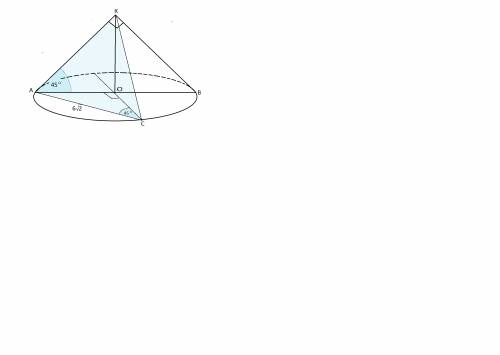
Найдите объем конуса, если хорда
его основания, равная 6√2,
отсекает четверть окружности основания,
а угол между образующей
и плоскостью основания равен 45°.
Объем конуса по классической формуле
V=1/3 S*H
Высота Н равна радиусу основания, т.к. образующая АК, АО радиус основания и высота КО составляют равнобедренный прямоугольный треугольник -
так как образующая с основанием составляет равнобедренный треугольник с углом при основании 45°.
Радиус найдем из равнобедренного прямоугольного треугольника, гипотенузой в котором данная в условии хорда - она отсекает четверть окружности, т.е дугу с центральным углом 360:4=90°.
Длина хордыАС= 6√2.
Соединив ее концы с центром окружности,
получим равнобедренный прямоугольный треугольник с катетами-радиусами основания.
Мы помним, что если гипотенуза равнобедренного прямоугольного треугольника равна а√2- катет равен а ( можно проверить по т.Пифагора).
Итак, радиус конуса - 6, высота- 6.
S=πr²=π6²=36π
V=1/3·36π·6=72 (единиц объема)
сечениями будут равнобокие трапеции, причем равные...
ребро пирамиды обозначим (а) а = 1
боковые грани пирамиды ---правильные треугольники...
одно основание трапеции = ребру пирамиды = а,
второе основание (меньшее) = средней линии боковой грани пирамиды = а/2
боковая сторона трапеции = медиане боковой грани пирамиды = а*V3 / 2
(высота трапеции)^2 = (а*V3 / 2)^2 - (a/4)^2 = 3a^2 / 4 - a^2 / 16 = 11a^2 / 16
высота трапеции = a*V11 / 4
если обозначить пересечение CF и BG как Е (и на противоположной грани пирамиды симметричную точку обозначить Е1), то ЕЕ1 ---линия пересечения плоскостей
ЕЕ1 || AB || CD
угол между плоскостями ---угол между перпендикулярами к ЕЕ1, лежащими в этих плоскостях (угол между отрезками высот трапеций),
причем этот угол ---угол при вершине O треугольника GOH, где точка О лежит на ЕЕ1, GO _|_ EE1, OН _|_ EE1, GO+OH = высоте трапеции, GH = а*V3/4
точка Е ---пересечение медиан равностороннего треугольника (боковой грани пирамиды) => точка Е разбивает медианы (а это боковая сторона трапеции...) в отношении 2:1, считая от вершины треугольника => и высота трапеции разбивается прямой ЕЕ1 на отрезки в отношении 2: 1, т.е. GO:OH = 1:2, т.е. OH = 2GO
GO = (a*V11 / 4) / 3 = a*V11 / 12
OН = 2*(a*V11 / 12) = a*V11 / 6
по т.косинусов из треугольника GOH
(GН)^2 = OH^2 + GO^2 - 2*OH*GH*cos(GOH)
3a^2 / 16 = 11a^2 / 36 + 11a^2 / 144 - (11a^2 / 36)*cos(GOH)
3a^2 / 16 - 11a^2 / 144 = (11a^2 / 36)*(1-cos(GOH))
1-cos(GOH) = 16a^2 / 144 : (11a^2 / 36) = 4/11
cos(GOH) = 1 - 4/11 = 7/11
искомый угол = arccos(7/11)
Множество таких центров окружностей (точек) лежат на биссектрисе данного угла. Любая точка биссектрисы лежит на равном удалении от сторон угла.