Площадь осевого сечения цилиндра равна 156 см^2. найдите высоту цилиндра, если радиус его основания равен 6 см.

👇

Увидеть ответ

Ответ:

evasaidova91

18.12.2022

Осевое сечение цилиндра прямоугольник. Sпрям=a*b, где а -ширина, а b- длина.
a = 6*2= 12
b= 156/12 = 13
ответ: 13

4,5(68 оценок)

Открыть все ответы

Ответ:

БлинчикТян

18.12.2022

Случай 1 : Площадь бо́льшего треугольника равна 8 (ед²).Отношение сходственных сторон подобных треугольников равно коэффициенту подобия.

Пусть S₁ - это площадь бо́льшего треугольника, а S₂ - площадь меньшего треугольника.

Пусть k > 1 (это значит, что в числителе будет стоять бо́льший треугольник).

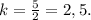
$k = \frac{5}{2} = 2,5.$

Площади подобных треугольников относятся как квадрат коэффициента подобия.

Отсюда -

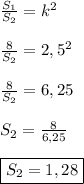
$\frac{S_{1} }{S_{2} } = k^{2} \\\\\frac{8}{S_{2} } = 2,5^{2} \\\\\frac{8}{S_{2} } = 6,25\\\\S_{2} = \frac{8}{6,25} \\\\\boxed{S_{2} = 1,28}$

1,28 (ед²).

- - -

Случай 2 - Площадь меньшего треугольника равна 8 (ед²).

В этом случае наоборот k < 1 (в числителе будет стоять меньший треугольник).

S₁ - площадь бо́льшего треугольника, S₂ - площадь меньшего треугольника

Тогда -

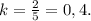
$k = \frac{2}{5} = 0,4.$

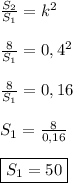
$\frac{S_{2} }{S_{1} } = k^{2}\\\\\frac{8 }{S_{1} } = 0,4^{2}\\\\\frac{8 }{S_{1} } = 0,16\\\\S_{1} = \frac{8}{0,16}\\\\\boxed{S_{1} = 50}$

50 (ед²).

4,8(24 оценок)

Ответ:

ЛехаФомин

18.12.2022

В обеих задачах один из углов в треугольнике = 120°. Этот угол не может быть углом при основании равнобедренного Δ, так как эти углы должны быть равными, и их сумма будет равна 240°, что больше, чем 180°.
Значит угол в 120° - это угол при вершине.
Углы при основании будут равны (180°-120°):3=30°
1) Опустим высоту из вершины А на бок. сторону ВС (АС - основание равнобедренного ΔАВС), получим точку Н. Она будет лежать на продолжении стороны ВС, т.к. ∠В=120° - тупой.
Рассм. ΔАНС: ∠АНС=90°, ∠АСН=30° ⇒ АН - катет, лежащий против угла в 30°, равен половине гипотенузы. Гипотенузой является АС=18 см.
АН=18:2=9 (см)

2) В этой задаче всё аналогично, чертёж такой же, только известно не АС, а АВ=ВС=14.
Чтобы найти высоту АН, как катет, лежащий против угла в 30° в ΔАНС, надо вычислить длину основания АС в равнобедренном ΔАВС
( АС является гипотенузой в ΔАНС) .
Теорема косинусов:
АС²=АВ²+ВС²-2·АВ·ВС·сos120°=14²+14²-2·14·14·cos(90°+30°)=
=2·14²-2·14²·(-cos30°)=2·14²·(1+√3/2)=2·14²·(2+√2)/2=14²·(2+√3)

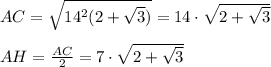
$AC=\sqrt{14^2(2+\sqrt3)}=14\cdot \sqrt{2+\sqrt3}\\\\AH=\frac{AC}{2}=7\cdot \sqrt{2+\sqrt3}$