Найдем гипотенузу прямоугольного треугольника.
√(6²+8²)=√100=10
Значит сторона правильного треугольника равна 10 см.
Найдем полупериметр правильного треугольника со стороной 10:
р=10*3/2=15 см
Найдем радиус вписанной в треугольник окружности:
r=√(p-10)³/p=√(125/15)=5/√3
ответ: 5/√3 см
Рассмотрим второй вариант, если бы в условии нужно было узнать возможно ли построить равносторонний треугольник внутри прямоугольного, не пересекающийся с исходным, одной стороной лежащий на гипотенузе и с вершиной, совпадающей с вершиной прямого угла и если возможно - найти радиус вписанной окружности в этот треугольник.
Решение: В равностороннем треугольнике все его внутренние углы равны 60°. поэтому, нужно убедиться, что оба непрямых угла прямоугольного треугольника меньше 60°. Для этого достаточно определить один уз углов, прилегающих к гипотенузе. Т.к. длины всех сторон уже известны (6, 8 и 10 см), найдем отношение катета длиной 8 к гипотенузе. 8/10=0,8. arcsin 0,8≈53°<60°, значит и второй угол 180-90-53≈37°<60°.
Делаем вывод, что треугольник с заданными параметрами вписать можно.
Очевидно, что высота, опущенная из вершины прямого угла на гипотенузу прямоугольного треугольника, совпадает с высотой искомого равностороннего треугольника. Найдем эту высоту.
h=6*sin(arcsin 0,8)=6*0.8=4.8 см
Найдем теперь сторону равностороннего треугольника с высотой 4,8 см.
а=4,8/sin60°=9.6/√3
Радиус вписанной в равносторонний треугольник окружности:
r=a/(2√3)=4,8/3=1,6
ответ: 1,6 см
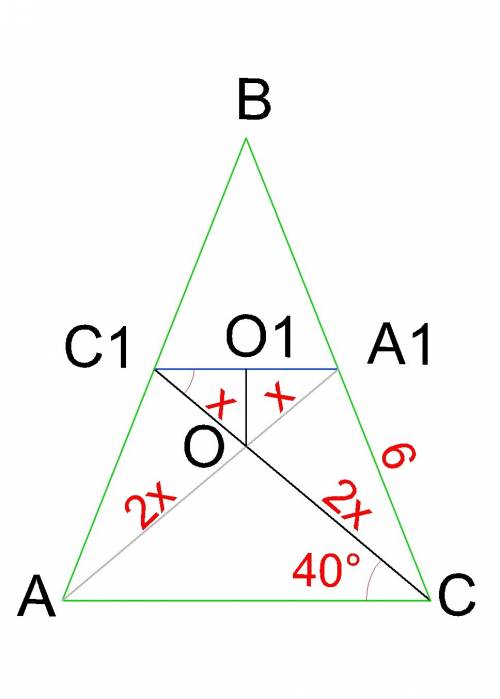
Проведем С₁А₁. С₁А₁║АС, так как АС₁=СА₁, ∠ВАС=∠АСВ (треугольник равнобедренный). Из параллельности С₁А₁║АС, следует, что СС₁ как секущая образует равные углы ∠АСС₁ = ∠СС₁А₁=40° (накрест лежащие углы).
Медианы равнобедренного треугольника точкой пересечения делятся на отрезки, соотношение длин которых 2:1, а так как АА₁=СС₁, то и отрезки ОС₁=ОА₁ и СО=АО. Обозначим стороны ОС₁=ОА₁ за х, тогда СО=АО=2х, а искомая медиана СС₁=3х.
Из точки О опустим высоту ОО₁ на С₁А₁. ОО₁ также является медианой ΔОС₁А₁, . Найдем С₁О₁ как катет прямоугольного ΔОС₁О₁.
С₁О₁=х·cosOC₁O₁=x·cos40°.
С₁А₁=2·С₁О₁=2x·cos40°.
По теореме косинусов из ΔСС₁А₁ найдем х.
6²=(2x·cos40°)²+9х²-2·3х·2x·cos40°·cos40°
36=х²·(9-8·cos²40°)
х=6/√(9-8·cos²40°)
СС₁=3х=18/√(9-8·cos²40°)≈8,67 см
ответ: СС₁=18/√(9-8·cos²40°)
(задача проверена графическим методом. всё совпало)
Дано: AB=BC, AO=BO=OC=25 см, AC=48 см.
Решение: см. на рисунок. Площадь треугольника ABC можно найти как 1/2*BH*AC. Найдем BH=BO+OH, BO известно, найдем OH. Треугльник COH прямоугольный (OH - высота), HС=1/2*AC (в равнобедренном треугольнике высота проведенная к основанию является и медианой). По теореме Пифагора найдем OH:
OC=25, HC=48/2=24. Подставим и получим OH=7 см. ВН=25+7=32.
S треугольника =1/2*48*32=768 (см квадратных).
ответ: 768 кв. см.