Так как ось правильной усеченной пирамиды совпадает с осью соответствующей полной пирамиды, то OO1 является высотой пирамиды и точки О и О1 являются центрами окружностей, вписанных в квадраты ABCD и A1B1C1D1. Тогда проведем ОК ⊥ AD и
OK1 ⊥ A1D1.
Значит, ОК и O1K1 — радиусы вписанных окружностей
Далее, проведем К1Н ⊥ KO. Из прямоугольника K1O1OH следует, что ОК = О1К1=1 м. Так что KH = KO OH = 4 1 = 3 (м.)
Далее, из прямоугольного ΔKK1H найдем по теореме Пифагора:
где КК1 — апофема.
Далее, площадь полной поверхности
ответ: 168 м2.
Объяснение
удачи!
Объяснение:
1) по теореме об угле в 30° в прямоугольном треугольнике CD=1\2AC=4
AC²=AD²+CD²
64=16+AD²
AD²=48 AD=4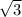
площадь равна AD*CD=16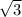
3) опускаем высоту ВЕ, тр-к АВЕ прямоугольный, ∠АВЕ=45°, значит АЕ=ВЕ=8-3=5
площадь= сумме площадей тр-ка АВЕ и пр-ка ВСDЕ=1/2*5*5+3*5=12,5
4) опускаем высоту ВЕ. тр-к АВЕ прямоугольный, ∠АВЕ=30°
по теореме об угле в 30°, АЕ=1\2АВ=2. АВ²=ВЕ²+АЕ² ВЕ=2√3
площадь = 1/2АС*ВЕ=1/2*6*2√3=6√3
5) опускаем высоту из угла В, она делит сторону АС пополам в точке Е
тр-к АВЕ прямоугольный и ВЕ=12.значит площадь тр-ка равна 1/2*ВЕ*АС=108
6) пусть НВ это х, тогда АН=7+х
площадь тр-ка АВС=сумме площадей тр-ков АСН и СНВ
площадь ΔАСН=1/2*12*(7+х)
площадьΔСНВ=1\2*12*х
АВ=х+7+х=2х+7
АС²=(7+х)²+144
ВС²=х²+144
АВ²=(2х+7)²=(х+7)²+144+х²+144
упрощаем х²+7х-144=0
находим корни через дискриминант
один из них отрицательный, другой =5,5
НВ=5,5, АН=12.5, площадьΔАВС=1\2*12*5,5+1/2*12*12,5=108