Рисунки.
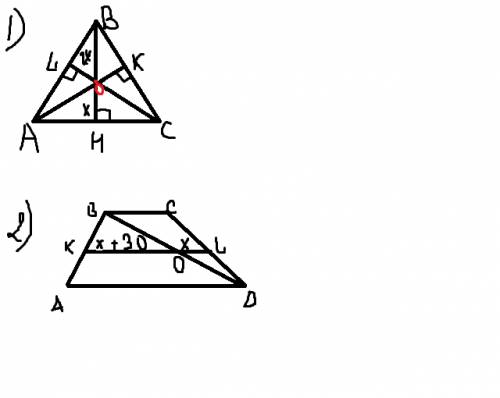
1) Дано: Треуг. АВС - равностор. Решение: Т.к. треуг. равносто-
ВН - высота ронний, то ВН=CL=AK
ВН=63 мм BH, CL, CK - высоты и бисс.
т.О- точка пересечения биссектрис В равностор. треуг. биссектр. в
Найти: ОН, ОL, ОК. точке пересечения делятся в отношении 1/2.
=> ВО=2х
ОН=х
ВО+ОН=ВН
3х=63
х=21 мм.
2) Решение: т.к. KL - сред.линия трапеции, KL=(BC+AD):2 (надо записать дробью)
=>BC=2KL-AD
Рассмотрим треуг.ABD, KO - сред. линия треуг.
=>KO=AD:2 (тоже дробь) =>AD=2KO
KO+OL=KL Пусть OL=x, тогда KO= х+30
х+30+х=110
х=40мм
AD=2KO=2*(x+30)=2*(40+30)=140мм
BC=2KL-AD=2*100-140=80мм
Дано: M, K, N ∈ a; MK = 7см; KN = 10см.
Найти: MN.
Решение: рассмотрим 3 различных случая.
1)
Если K ∈ MN:
MN = MK + KN = 7 + 10 = 17см.
2)
Если M ∈ KN:
MN = KN - KM = 10 - 7 = 3см.
3)
Если N ∈ KM:
Получается противоречие: KN < KM, но по условию KN > KM. Такой случай невозможен.
ответ: 17см или 3см.