Если вспомнить, что величина, умноженная на корень из двух, это в то же время формула диагонали квадрата d=а√2 и гипотенузы равнобедренного прямоугольного треугольника, то нетрудно будет узнать величину искомого угла.
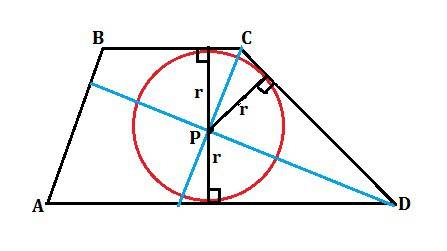
Соедимим концы В и С хорды с центром окружности.
Радиусы окружности и хорда образуют прямоугольный равнобедренный треугольник СОВ
( см. рисунок вложения).
Выбрав на дуге ВС произвольно точку А, соединим ее с В и С.
∠ ВАС вписанный и равен половине центрального угла ВаС.
∠ВаС=360°-90°=270°, следовательно,
∠ВАС=270°:2=135°
Отметим, что величина этого угла не зависит от местоположения точки А по отношению к В и С.
∠ВАС=∠ВА₁С, как и любому углу, вершина которого будет лежать на этой же дуге, а концы угла опираться на дугу ВаС.

V = 84 см³.
Объяснение:
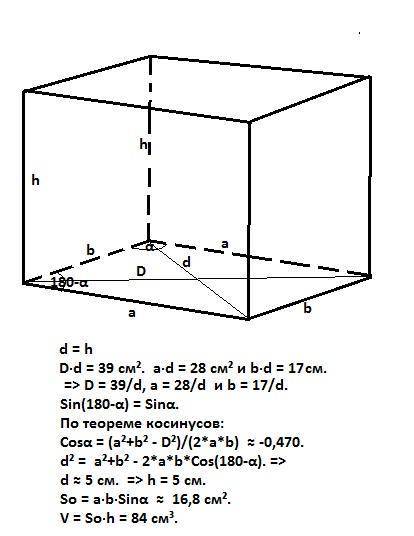
Основание - параллелограмм. Стороны а и b. Диагонали D и d.
Одна из диагоналей (например, d) равна высоте параллелепипеда (дано).
Тогда имеем соотношения:
D·d = 39 см². a·d = 28 cм² и b·d = 17. =>
D = 39/d, a = 28/d и b = 17/d.
В параллелограмме углы, прилежащие к одной стороне, в сумме равны 180°. Заметим, что Sin(180-α) = Sinα.
По теореме косинусов для треугольника но диагонали D:
Cosα = ((28/d)² + (17/d)² - (39/d)²)/(2·(28/d)·(17/d) ≈ -0,470. (d² в числителе и знаменателе сокращаются).
Снова по теореме косинусов (теперь уже для треугольника на диагонали d c острым углом 180-α - по свойству углов параллелограмма):
d² = (28/d)² + (17/d)² - 2· (28/d)· (17/d)·0,470 =>
d^4 = 28²+17²-2·17·28·0,470 => d ≈ 5 см. => h = 5 см.
So = a·b·Sinα = 5,6·3,4·√(1 - 0,470²) ≈ 16,8 см².
Тогда V = So·h = 16,8·5 = 84 см³.
Проведём перпендикуляры РК, РН и РМ к сторонам ВС, СД и АД соответственно.
Треугольники КРС и НРС равны, так как ∠КСР=∠НСР, оба прямоугольные и сторона СР - общая, значит КР=НР.
Аналогично доказывается равенство тр-ков НРД и МРД. В них МР=НР.
Доказано,что КР=НР=МР, задача решена.