Проведем касательные, образующие угол 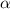 . В точки касания проведем радиусы из центра соответствующей окружности. Теперь проведем искомое расстояние между точками касания.
. В точки касания проведем радиусы из центра соответствующей окружности. Теперь проведем искомое расстояние между точками касания.
Рассмотрим четырехугольник, образованный касательными и радиусами.. Из него нам нужно найти угол 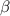 . Так как два угла этого четырехугольника равны 90, то находим выражение для b: b=180-a.
. Так как два угла этого четырехугольника равны 90, то находим выражение для b: b=180-a.
Далее рассмотрим треугольник, образованный двумя r и d. По теореме косинусов находим сначала квадрат d, а потом и само d (в процессе была использована формула приведения: cos(180-a)=-cos(a) )
Воспользуемся следующими соотношениями в прямоугольных треугольниках:
Синусом острого угла называется отношение противолежащего катета к гипотенузе.
Котангенсом острого угла называется отношение прилежащего катета к противолежащему.
ΔМАО=ΔМВО по катету (МА=МВ) и гипотенузе (МО- общая сторона)
ΔМАК=ΔМВК (МК-общий катет, МА=МВ - гипотенузы)
Из ΔМАО находим МА:

Из ΔМАК находим АК:

Если же такой ответ не годится и нужно выразить именно через α, то по формуле половинного аргумента получим:

Ну и как "Лучшее решение" не забудь отметить, ОК?!.. ;)))
Sосн.=1/2*6*8=24 см²
Найдем третью сторону треугольника по теореме Пифагора. c²=a²+b²
c²=6²+8²
c²=36+64
c²=100
c=10 см
Периметр основания Р=6+8+10=24 см
Sбок.=P*H=24*10=240 см²
S полн=2*24+240=48+240=288 см²