постарался объяснить максимально возможно
Объяснение:
По теореме о 3х перпендикулярах:
Прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость.
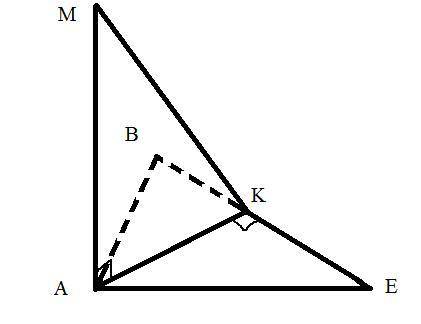
В данном случае MA⊥АК, так как MA⊥ABE (прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости).
Значит MK - наклонная, а АК - её проекция.
При этом, т.к. △АВЕ равносторонний, то медиана АК также является высотой, т.е. АК⊥ВЕ.
Получается, что ВЕ перпендикулярна проекции наклонной МК, значит по теореме о 3х перпендикулярах МК⊥ВЕ, чтд.
AC∩BD=0
BO=k/2
<BAO=a/2
<BAO=90-a/2
BO/sin<BAO=AO/sin<ABO
AO=BO*sin<ABO/sin<BAO=k*sin(90-a/2)/(2sina/2)=k*cosa/2/(2sina/2)=
=1/2*kctga/2
AC=2AO=kctga/2
S=AC*BD/2=1/2*k*kctga/2=1/2*k²ctga/2