1) 1м.
2) 21 кв. ед.
3) 34.25 кв. ед.
Объяснение:
Дано. Стороны грядки, имеющей форму прямоугольника, равны 2,5 м и 0,4м.
Найти периметр грядки, равновеликой данной и имеющей форму квадрата.
Решение.
Равновеликие прямоугольник и квадрат у которых равные площади.
Найдем площадь прямоугольника
S=ab = 2.5 * 0.4 = 1 м².
S квадрата = S прямоугольника
S квадрата =a²; a²=1;
a=±1; (-1 - не соответствует условию.)
а=1 м.
Равновеликим прямоугольнику со сторонами 2,5 м и 0,4 м является квадрат со стороной 1 м.
***
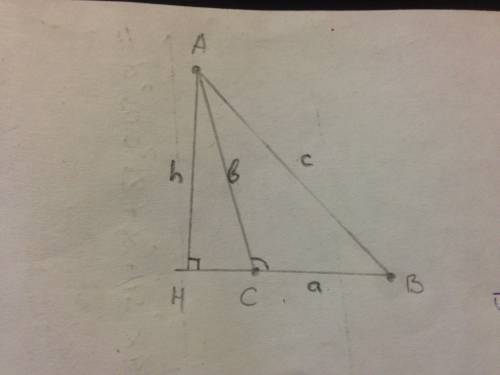
2) Дано. ABCD - трапеция. AB=6; BC=4; AD=10; угол A=30*.
Найти площадь.
Решение.
Проведем высоту ВЕ. Получили треугольник АВЕ, в котором угол А=30* АВ=6 - гипотенуза. АЕ и ВЕ - катеты, а ВЕ=h - еще и высота трапеции.
BE =h = AB* sin 30*=6*1/2=3.
Площадь S=h(a+b)/2 = 3*(10+4)/2=3*14/2=21 кв. ед.
***
3) Дано. Δ ACD, у которого ∠А=30°; ∠ACB=60°; внешний угол D = 135°; BC=5 - высота. Найти площадь.
Решение.
В Δ BCD внутренний угол В = 180°-135° = 45°. Следовательно Δ BCD - равнобедренный ВС=BD = 5.
Из Δ АВС АВ = ВС/ tg30° = 5/0.577 = 8,7.
AD = 8,7 + 5=13,7.
Площадь S=1/2*AD*BC = 1/2* 13.7*5 = 34.25 кв. ед.
Вариант 2.
1). «Две прямые не пересекаются, если соответственные углы равны»? Верно
Если соответственные углы равны, прямые параллельны.
2). « Существует треугольник, один из углов которого равен разности двух других»? Верно
Это прямоугольный треугольник; угол А=90 градусов, угол С=А-В=90-В
3). «Если сторона и 2 угла одного треугольника равны стороне и 2-м углам другого треугольника, то треугольники равны»? неверно, такие треугольники подобны;
Если сторона и 2 прилегающих к ней угла одного треугольника равны стороне и
2-м прилегающим к ней углам другого треугольника, то треугольники равны
4). «В прямоугольном треугольнике сумма острых углов не меньше 90 градусов»? Верно
она равна 90
5). «Треугольник с двумя различными острыми внешними углами не существует»? Верно,
поскольку острый внешний угол означает, что смежный с ним угол треугольника
будет тупым, а у треугольника может быть только один тупой угол.
6). «В треугольнике РМЕ , ,сторона РЕ- наименьшая». что-то пропущено в условии вопроса;
если, например, угол М наименьший, то и сторона РЕ наименьшая, поскольку она
лежит напротив наименьшего угла.
В заданиях 7-9 поясните ответ.
7). В равнобедренном треугольнике один из углов равен 800 .Чему равны остальные углы?
сумма углов треуг 180. В равнобедренном треуг два одинаковых угла,
если они по 80, то третий равен 180-80-80=20; если же это угол при вершине,
то углы при основании равны (180-80)/2=50 градусов
8). В треугольнике одна из сторон равна 8 см, другая – 10 см. Какие целочисленные значения может принимать длина третьей стороны? сумма длин сторон треугольника всегда больше
длины третьей стороны, то есть третья сторона меньше 8+10=18,
и она может принимать любое целое значение, от 1 см по 17 см
9). В прямоугольном треугольнике наибольшая сторона МТ=39, МК=19,5. Чему равен
вопрос не сформулирован
2 часть
1). Внутри равностороннего треугольника АВС отмечена точка К, такая, что углы ВАК и ВСК равны 150. Найдите АКС. ( ) В условии что-то напутано, не могут ВАК и ВСК равнятья 150 градусов
2). Длины двух сторон равнобедренного треугольника равны соответственно 3 см и 1 см. Определите длину третьей стороны этого треугольника. ( ) В равнобедр треуг две одинаковых стороны. Если это стороны по 3 см, то такой треугольник существует, выполняется условие, что сумма двух сторон треуг больше его третьей стороны. Если бы 2 одинаковые стороны были бы по 1 см, то это условие не выполнится, 1+1<3, значит, такого треуг не существует. ответ: третья сторона длиной 3 см
3). В равнобедренном треугольнике с боковой стороной, равной 14 см и углом 1500 найдите высоту, проведенную к боковой стороне. ( )
4). Докажите, что любая сторона треугольника меньше суммы двух других сторон. ( )
не знаю, как у вас в учебнике, можно просто нарисовать
длинную сторону и "положить" на нее с каждого края отрезки, сумма которых равна
этой стороне или меньше ее, сразу станет понятно.
Объяснение:
Найдем площадь треугольника по формуле Герона
Подставим получившееся значение в первое уравнение
Замена
Вернемся к замене
Найдем больший угол треугольника по теореме косинусов
1) Стороны: 3; 4; 3,5
Значит ∠B < 90° ⇒ ΔABC - остроугольный.
2) Стороны: 3; 4; 2
Значит ∠B > 90° ⇒ ΔABC - тупоугольный.
По условию треугольник тупоугольный, значит AB = 2, а P = 3 + 4 + 2 = 9
ответ: 9