Sabc = 384 см².
Объяснение:
Так как точка S равноудалена от вершин треугольника АВС, она проецируется в центр описанной окружности этого треугольника - точку О. А так как треугольник АВС прямоугольный, то этот центр находится на середине гипотенузы АВ. Точка J по этой же причине находится на отрезке SO, перпендикулярном плоскости АВС. АО = ВО = СО как радиусы описанной окружности.
JO = SO - SJ = 40 - 25 = 15 см. Тогда в треугольнике CJO по Пифагору
СО = √(CJ²-JO²) = √(25²-15²) = 20 cм. АВ = 2·СО = 40 см.
Это гипотенуза. Второй катет равен по Пифагору:
АС = √(АВ²-ВС²) = √(40²-24²) = 32 см.
Площадь треугольника АВС равна
Sabc = (1/2)·АС·ВС = (1/2)·32·24 = 384 см².

S = 675√3 см².
Объяснение:
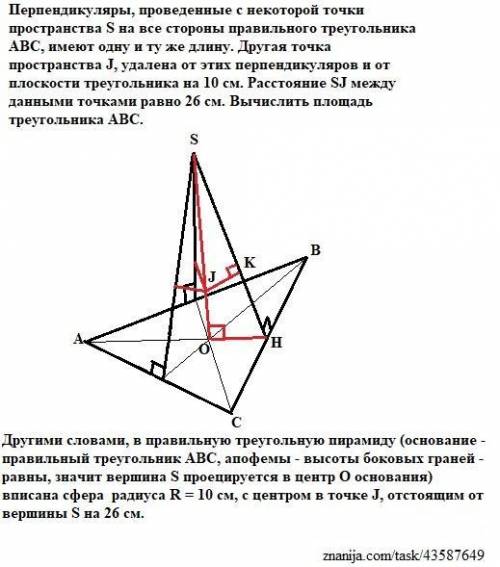
Задача: Перпендикуляры, проведенные с некоторой точки пространства S на все стороны правильного треугольника ABC, имеют одну и ту же длину. Другая точка пространства J, удалена от этих перпендикуляров и от плоскости треугольника на 10 см. Расстояние SJ между данными точками равно 26 см. Вычислить площадь треугольника.
Другими словами, в правильную треугольную пирамиду (основание - правильный треугольник АВС, апофемы - высоты боковых граней - равны, значит вершина S проецируется в центр О основания) вписана сфера радиуса R = 10 cм, с центром в точке J, отстоящим от вершины S на 26 см.
В прямоугольном треугольнике SKJ по Пифагору найдем катет SK = √(SJ²-JK²) = √(26²-10²) = 24 см.
Прямоугольные треугольники SKJ и SOH подобны по острому углу OSH - общий. SO = SJ + JO = 26+10 = 36 см. Из подобия имеем:
SO/SK = OH/JK.
OH = JK·SO/SK = 10·36/24 = 15 см.
Отметим, что ОН = (1/3)·АН так как точка О - центр правильного треугольника, точка пересечения его высот и медиан. Тогда АН = 15·3 = 45 см. Это высота треугольника АВС.
Тогда по известной формуле h = (√3/2)·a находим сторону треугольника.
а = 45·2/√3 = 30√3 см.
Площадь правильного треугольника равна S = (√3/4)·a².
S = (√3/4)·(30√3)² = 2700·√3/4 = 675√3 см².