Дано :
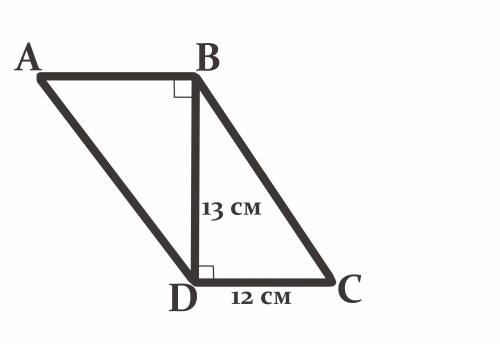
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
т.к. СК - высота, АН/АС = cosBAC
AH = AC*cosBAC=0.25* 2√15 = (√15)/2
AB = 2AH = √15
Треугольник АНВ, угол АНВ = 90',
т.к. АН - высота, cosBAC = cosABC = 0.25
sinABC = √(1-cos^2ABC) = √(1-1/4^2) = (√15)/4
AH/AB = sinABC AH = AB*sinABC = √15*(√15)/4 = 154 = 3.75
ответ: высота АН равна 3.75.