ответ: 90° и 36°
Объяснение: Очевидно, что для составления из двух равнобедренных треугольников другого, нужно:
чтобы их боковые стороны были равны; чтобы угол одного при составлении дополнял до развернутого угла угол другого (В противном случае получится четырехугольник).Возможны два варианта решения.
1. Такой треугольник можно составить из равных равнобедренных прямоугольных треугольников Их острые углы равны 45°, и угол между боковым сторонами нового треугольника будет 90°. ( см. рисунок вложения)
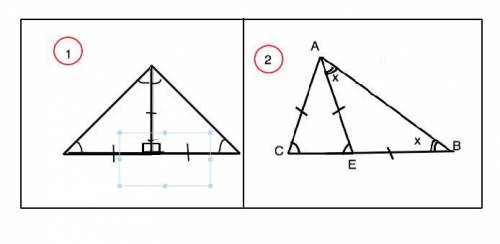
2. Обозначим исходные треугольники АВЕ и АСЕ ( АЕ=ВЕ и АЕ=АС). В новом треугольнике АВС АВ=ВС, углы при АС равны. Угол при С общий для обоих треугольников. Треугольники АСЕ и АВС подобны по равным углам при АС. поэтому угол САЕ=углу АВС.
Примем угол АВЕ=ВАЕ= х, тогда угол ВЕА=180°-2х.
=> Смежный с ним угол АЕС=2х, равный ему угол ЕСА=АЕС=2х. В ∆ АВС сумма углов В+А+С=х+2х+2х=180°
5х=180° => х=180°:5=36°
ответ: 90° и 36°
Объяснение: Очевидно, что для составления из двух равнобедренных треугольников другого, нужно:
чтобы их боковые стороны были равны; чтобы угол одного при составлении дополнял до развернутого угла угол другого (В противном случае получится четырехугольник).Возможны два варианта решения.
1. Такой треугольник можно составить из равных равнобедренных прямоугольных треугольников Их острые углы равны 45°, и угол между боковым сторонами нового треугольника будет 90°. ( см. рисунок вложения)
2. Обозначим исходные треугольники АВЕ и АСЕ ( АЕ=ВЕ и АЕ=АС). В новом треугольнике АВС АВ=ВС, углы при АС равны. Угол при С общий для обоих треугольников. Треугольники АСЕ и АВС подобны по равным углам при АС. поэтому угол САЕ=углу АВС.
Примем угол АВЕ=ВАЕ= х, тогда угол ВЕА=180°-2х.
=> Смежный с ним угол АЕС=2х, равный ему угол ЕСА=АЕС=2х. В ∆ АВС сумма углов В+А+С=х+2х+2х=180°
5х=180° => х=180°:5=36°

По свойству касательной и секущей ОК²=ОМ·ОN.
Пусть ОМ=х, тогда ОN=OM+MN=x+6,
4²=x(х+6),
х²+6х-4=0,
х1=-8, отрицательное значение не подходит,
х2=2.
ON=2+6=8 дм - это ответ.
Теперь докажем, что отрезок MN виден из точки К под большим углом.
Пусть радиус окружности около тр-ка КMN равен r.
На стороне ОК в любом месте возьмём точку Р и опишем окружность около тр-ка РMN, радиусом R. ОР для неё является секущей, а для окружности, радиусом r - касательной, значит R>r.
Формула хорды: l=2R·sin(x/2), где х - градусная мера хорды.
∠MKN=α, ∠MPN=β.
Обратим внимание, что углы α и β - это половина градусной меры хорды.
MN=2R·sinβ ⇒ sinβ=MN/2R.
MN=2r·sinα ⇒ sinα=MN/2r.
Сравним синусы, предположив, что они равны.
MN/2R=MN/2r.
1/R=1/r, но R>r, значит 1/R<1/r, значит sinβ<sinα.
Так как градусная мера хорды не может быть больше 180°, значит в формуле хорды 0°<α<90°, 0°<β<90°.
В этом диапазоне синус угла тем больше, чем больше его градусная мера,
значит α>β.
Доказано.