Объяснение:
№1 фото
Условие некорректно! Скорее всего надо было найти угол С.
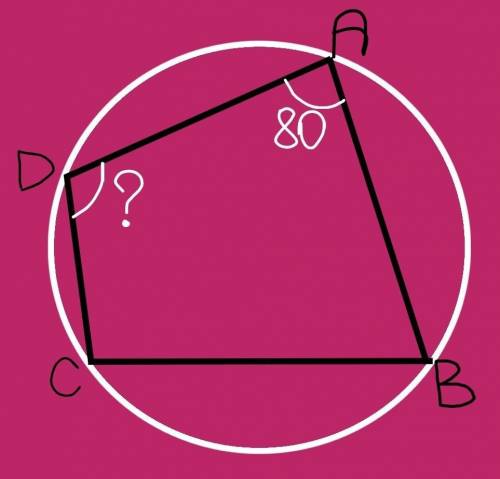
Около четырехугольника можно описать окружность, если сумма его противоположных углов равна 180°.
Углу А противоположен угол С, тогда угол С=180°–угол А=180°–80°=100°.
ответ: б) 100°
Найти угол D, незная угол В или не имея других данных, невозможно.
№2
Около четырехугольника можно описать окружность, если сумма его противоположных углов равна 180°.
Тогда угол CDA=180°–угол АВС=180°–110°=70°.
Сумма углов в любом треугольнике равна 180°.
Следовательно угол ACD=180°–угол CAD–угол CDA=180°–50°–70°=60°
ответ: в) 60°
№3
В четырехугольник можно вписать окружность, если суммы его противоположных сторон равны.
Тоесть ВС+AD=AB+CD
Пусть АВ=4n, тогда CD=3n.
Подставим значения в уравнение:
13+22=4n+3n
35=7n
n=5
Тогда CD=3*5=15 см
ответ: а) 15 см.
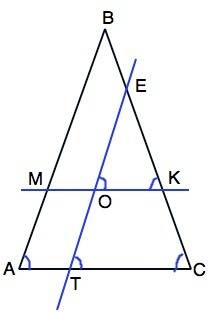
В равнобедренном треугольнике углы при основании равны. ∠ВАС=∠ВСА
Обозначим данный треугольник АВС; О - точку пересечения прямых ЕТ||АВ и МК||АС.
АС секущая при ВА║ЕТ ⇒
∠ЕТС=∠ВАС как соответственные.
ЕТ секущая при МК║АС⇒
∠ЕОК=∠ЕТС как соответственные, следовательно, ∠ЕОК=∠ВАС.
ВС секущая при МК||АС⇒
∠ЕКО=∠ВСА, как соответственные. .
Следовательно, ∠ЕКО=∠ЕОК. что является признаком равнобедренного треугольника. ⇒
Треугольник ЕОК равнобедренный с углами при основании, которые равны углам при основании АС треугольника АВС.
1) х + х + 64 = 180
2х + 64 = 180
2х = 180 - 64
2х = 116
х = 58
1 сторона - 58, 2 сторона - 122
2) х + 3х = 180
4х = 180
х = 45
1 сторона - 45, вторая - 135
3) х + х+56 = 180
2х+56 = 180
2х = 180-56
2х = 124
х = 62
1 сторона - 62, 2 сторона - 118