S = 24 cм².
Объяснение:
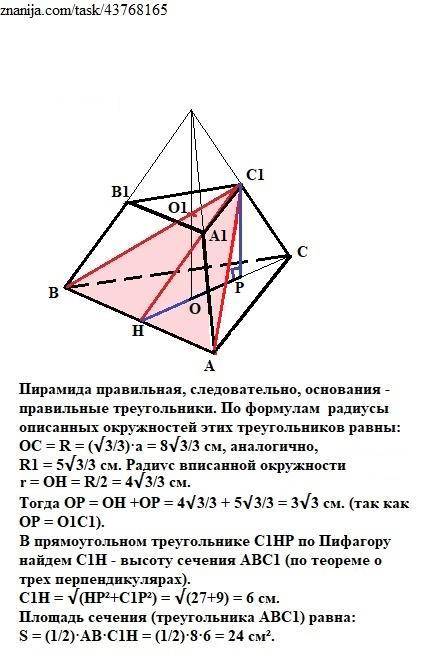
Пирамида правильная, следовательно, основания - правильные треугольники. По формулам радиусы описанных окружностей этих треугольников равны: ОС = R = (√3/3)·а = 8√3/3 см, аналогично,
R1 = 5√3/3 см. Радиус вписанной окружности r = OH = R/2 = 4√3/3 см.
Тогда ОР = ОН +ОР = 4√3/3 + 5√3/3 = 9√3/3 = 3√3 см. (так как ОР = О1С1).
В прямоугольном треугольнике С1НР по Пифагору найдем С1Н - высоту сечения АВС1 (по теореме о трех перпендикулярах).
С1Н = √(НР²+С1Р²) = √(27+9) = 6 см.
Площадь сечения (треугольника АВС1) равна:
S = (1/2)·AB·C1H = (1/2)·8·6 = 24 cм².
а) если равнобедренные треугольники имеют по равному острому углу при основании, то значит равны и вторые углы при основании и треугольники подобны. Если равны углы при вершине, то следовательно равны и углы при основании. Треугольники подобны.
б) Тупым может быть только угол при вершине. Тогда равны и углы при основании. Треугольники подобны.
в) В равнобедренных прямоугольных треугольников острые углы равны по 45 градусов. Треугольники подобны.