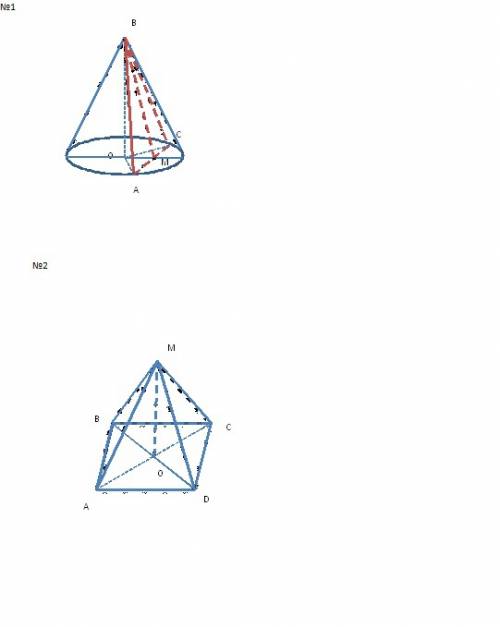
Вопросы к зачёту по 8 класс (л. с. атанасян и др.)1. параллелограмм. свойства параллелограмма(док-во)2. признаки параллелограмма (док-во)3. трапеция.4. прямоугольник. свойства прямоугольника(док-во)5. признак прямоугольника (док-во)6. ромб. свойство диагоналей ромба(док-во)7. квадрат8. площадь прямоугольника (док-во)9. площадь параллелограмма(док-во)10. площадь треугольника (док-во)11. площадь трапеции (док-во)12. теорема пифагора (док-во)13. определение подобных треугольников. теорема об отношенииплощадей подобных треугольников(док-во)14. первый признак подобия треугольников(док-во)15. второй признак подобия треугольников (док-во)16. третий признак подобия треугольников (док-во)17. средняя линия треугольника. свойство средней линиитреугольника (док-во)18. пропорциональные отрезки в (док-во)19. определение синуса, косинуса, тангенса и котангенса острогоугла прямоугольного треугольника20. значения синуса, косинуса, тангенса и котангенса для углов30,60,45 градусов ( с выводом)21. взаимное расположение прямой и окружности22. определение касательной. свойство и признак касательной23. теорема об отрезках касательной(док-во)24. центральные и вписанные углы. свойств(док-во)25. теорема о произведении отрезков пересекающихся хорд (док-во)26. свойство биссектрисы угла (док-во) и с рисунком .
Решение: Рассмотрим треугольник ACH: Так как CH - высота,то этот треугольник прямоугольный. Следовательно CH - катет и мы находим его по теореме Пифагора: CH = √6^²-4^² = √36-16 = √20 = 2√5
Я предлагаю рассмотреть треугольник ABC и найти x через CB(не знаю можно ли так,как я решил,но я запишу)
AB=4+x
CB=√AB²-AC² = √(4-x)²-6² = √x²-10x-20
Разбираем квадратичное уравнение:
x²-10x-20=0
D= 100+4*20=180 √D= 6√5
x_{12} = 5+-3√5
x2 - не подходит,так как получается отрицательным,поэтому BH = 5+3√5.
ответ: 5+3√5